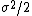“Volatility tax”的意思、由来-开放百科全书

词条

Volatility tax

释义

Overview
See also
References

The volatility tax is a mathematical finance term, formalized by hedge fund manager Mark Spitznagel, describing the effect of large investment losses (or volatility) on compound returns.^[1] It has also been called “volatility drag”.^[2]

Overview

As Spitznagel wrote:

{{quote|It is well known that steep portfolio losses crush long-run compound annual growth rates (CAGRs). It just takes too long to recover from a much lower starting point: lose 50% and you need to make 100% to get back to even. I call this cost that transforms, in this case, a portfolio’s +25% average arithmetic return into a zero CAGR (and hence leaves the portfolio with zero profit) the “volatility tax”: it is a hidden, deceptive fee levied on investors by the negative compounding of the markets’ swings.^[1]}}

Quantitatively, the volatility tax is the difference between the arithmetic and geometric average (or “ensemble average” and “time average”) returns of an asset or portfolio. It thus represents the degree of “non-ergodicity” of the geometric average.

Standard quantitative finance assumes that a portfolio’s net asset value changes follow a geometric Brownian motion (and thus are log-normally distributed) with arithmetic average return (or “drift”) , standard deviation (or “volatility”) , and geometric average return

So the geometric average return is the difference between the arithmetic average return and a function of volatility. This function of volatility

represents the volatility tax. (Though this is under the assumption of log-normality, the volatility tax is in fact independent of the assumed or actual return distribution.)

The mathematics behind the volatility tax is such that a very large portfolio loss has a disproportionate impact on the volatility tax that it pays and, as Spitznagel wrote, this is why the most effective risk mitigation focuses on large losses:

{{quote|We can see how this works by considering that the compound (or geometric) average return is mathematically just the average of the logarithms of the arithmetic price changes. Because the logarithm is a concave function (it curves down), it increasingly penalizes negative arithmetic returns the more negative they are, and thus the more negative they are, the more they lower the compound average relative to the arithmetic average—and raise the volatility tax.^[3]}}

According to Spitznagel, the goal of risk mitigation strategies is to solve this “vexing non-ergodicity, volatility tax problem” and thus raise a portfolio’s geometric average return, or CAGR, by lowering its volatility tax (and “narrow the gap between our ensemble and time averages”).^[3] This is “the very name of the game in successful investing. It is the key to the kingdom, and explains in a nutshell Warren Buffett’s cardinal rule, ‘Don’t lose money.’”^[4] Moreover, “the good news is the entire hedge fund industry basically exists to help with this—to help save on volatility taxes paid by portfolios. The bad news is they haven't done that, not at all.”^[3]

As Nassim Nicholas Taleb wrote in his 2018 book Skin in the Game, “more than two decades ago, practitioners such as Mark Spitznagel and myself built our entire business careers around the effect of the difference between ensemble and time.”^[5]

References

1. ^¹Not all risk mitigation is created equal, Pensions & Investments, November 20, 2017
2. ^https://blogs.cfainstitute.org/investor/2015/03/23/the-myth-of-volatility-drag-part-1/
3. ^¹²Thanks to volatility, you can’t always get what you want in investing, Pensions & Investments, March 9, 2018
4. ^[https://www.scribd.com/document/370967187/Universa-Mark-Spitznagel-Volatility-Tax The Volatility Tax], Universa Investments, February 2018
5. ^{{cite book|last1=Taleb|first1=Nassim Nicholas|title=Skin in the Game: Hidden Asymmetries in Daily Life|date=2018|publisher=Random House|isbn=9780425284629|language=en}}

4 : Interest|Mathematical finance|Exponentials|Risk management

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Overview

See also

References