“V-topology”的意思、由来-开放百科全书

词条

V-topology

释义

Definition
Examples
Variant
See also
References

In mathematics, especially in algebraic geometry, the v-topology (also known as the universally subtrusive topology) is a Grothendieck topology whose covers are characterized by lifting maps from valuation rings.

This topology was introduced by {{harvtxt|Rydh|2010}} and studied further by {{harvtxt|Bhatt|Scholze|2017}}, who introduced the name v-topology, where v stands for valuation.

Definition

A universally subtrusive map is a map f: X → Y of quasi-compact, quasi-separated schemes such that for any map v: Spec (V) → Y, where V is a valuation ring, there is an extension (of valuation rings) 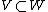and a map Spec W → X lifting v.

Examples

Examples of v-covers include faithfully flat maps, proper surjective maps.

{{harvtxt|Voevodsky|1996}} introduced the h-topology. It is based on submersive maps, i.e., maps whose underlying map of topological spaces is a quotient map (i.e., surjective and a subset of Y is open if and only if its preimage in X is open). Any such submersive map is a v-cover. The converse holds if Y is Noetherian, but not in general.

Variant

{{harvtxt|Bhatt|Mathew|2018}} have introduced the arc-topology, which is similar in its definition, except that only valuation rings of rank ≤ 1 are considered in the definition.

References

{{citation|title=The arc-topology|year=2018|first=Bhargav|last=Bhatt|first2=Akhil|last2=Mathew|arxiv=1807.04725v2}}
{{citation|first1=Bhargav|last1=Bhatt|first2=Peter|last2=Scholze||title=Projectivity of the Witt vector affine Grassmannian|journal=Inventiones Mathematicae|volume=209|year=2017|issue=2|pages=329–423|mr=3674218|doi=10.1007/s00222-016-0710-4|arxiv=1507.06490}}
{{citation|first1=David|last1=Rydh|title=Submersions and effective descent of étale morphisms|journal=Bull. Soc. Math. France|volume=138|year=2010|issue=2|pages=181–230|mr=2679038|arxiv=0710.2488}}

{{citation|title=Homology of schemes|author=Voevodsky|first=Vladimir|journal=Selecta Mathematica. New Series|volume=2|year=1996|issue=1|pages=111–153|mr=1403354|doi=10.1007/BF01587941}}

1 : Algebraic geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Definition

Examples

Variant

See also

References