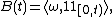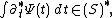1. White noise measure
     Brownian motion in white noise analysis  

2. Hilbert space
     Wick polynomials    Gelfand triples  

3. T- and S-transform
     Characterization theorem 

4. Calculus

5. Stochastic integrals

6. Applications

7. References

In probability theory, a branch of mathematics, white noise analysis is a framework for infinite-dimensional and stochastic calculus, based on the Gaussian white noise probability space, to be compared with Malliavin calculus based on the Wiener process.^[1] It was initiated by Takeyuki Hida in his 1975 Carleton Mathematical Lecture Notes.^[2]

The term white noise was first used for signals with a flat spectrum.

White noise measure

The white noise probability measure on the space of tempered distributions has the characteristic function^[3]

Brownian motion in white noise analysis

A version of Wiener's Brownian motion is obtained by the dual pairing

where is the indicator function of the interval . Informally

and in a generalized sense

Hilbert space

Fundamental to white noise analysis is the Hilbert space

generalizing the Hilbert spaces to infinite dimension.

Wick polynomials

An orthonormal basis in this Hilbert space, generalizing that of Hermite polynomials, is given by the so-called "Wick", or "normal ordered" polynomials with and

with normalization

entailing the Itô-Segal-Wiener isomorphism of the white noise Hilbert space 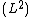with Fock space:

The "chaos expansion"

in terms of Wick polynomials corresponds to the expansion in terms of multiple Wiener integrals. Brownian martingales are characterized by kernel functions 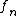depending on only by a "cut off":

Gelfand triples

Suitable restrictions of the kernel functions to be smooth and rapidly decreasing in and give rise to spaces of white noise test functions , and, by duality, to spaces of generalized functions of white noise, with

generalizing the scalar product in 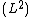. Examples are the Hida triple, with

or the more general Kondratiev triples.^[4]

T- and S-transform

Using the white noise test functions

one introduces the "T-transform" of white noise distributions by setting

Likewise, using

one defines the "S-transform" of white noise distributions by

It is worth noting that for generalized functions , {{clarify|text=with kernels as in ,|reason=As in what?|date=May 2018}} the S-transform is just

Depending on the choice of Gelfand triple, the white noise test functions and distributions are characterized by corresponding growth and analyticity properties of their S- or T-transforms.^[3][4]

Characterization theorem

The function is the T-transform of a (unique) Hida distribution iff for all the function is analytic in the whole complex plane and of second order exponential growth, i.e. where is some continuous quadratic form on .^[3][5][6]

Calculus

For test functions , partial, directional derivatives exist:

where 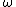may be varied by any generalized function . In particular, for the Dirac distribution one defines the "Hida derivative", denoting

Gaussian integration by parts yields the dual operator on distribution space

An infinite-dimensional gradient

is given by

The Laplacian ("Laplace–Beltrami operator") with

plays an important role in infinite-dimensional analysis and is the image of the Fock space number operator.

Stochastic integrals

A stochastic integral, the "Hitsuda-Skorohod integral" can be defined for suitable families of white noise distributions as a Pettis integral

generalizing the Itô integral beyond adapted integrands.

Applications

In general terms, there are two features of white noise analysis which have been prominent in applications.^{[7][8][9][10][11]}

First, white noise is a generalized stochastic process with independent values at each time.^[12] Hence it plays the role of a generalized system of independent coordinates, in the sense that in various contexts it has been fruitful to express more general processes occurring e.g. in engineering or mathematical finance, in terms of white noise.^[13][9][10]

Second, the characterization theorem given above allows various heuristic expressions to be identified as generalized functions of white noise. This is particularly effective to attribute a well-defined mathematical meaning to so-called "functional integrals". Feynman integrals in particular have been given rigorous meaning for large classes of quantum dynamical models.

Noncommutative extensions of the theory have grown under the name of quantum white noise, and finally, the rotational invariance of the white noise characteristic function provides a framework for representations of infinite-dimensional rotation groups.

References

• Apreta
• A. pretrei
• A. pretrei (disambiguation)
• Aprevalia
• Aprey
• APR formula
• A Price Above Rubies
• Apricitabine
• Apricoke
• Apricosiren
• Apricot-breasted
• Apricot jelly
• Apricot kernel biscuits
• Apricot mallow
• Apricot (open game)
• Apricot Picobook Pro
• Apricot Stone
• Apricot, Washington
• Apriday
• Apridi
• Apries River
• A Priest Walks Into a Bar
• Apriki Manor
• APRIL
• April 0