- Early life
- Academic career
- Mathematical results
- Papers
- Notes
- References
|name = Winifred Sargent
|image =
|image_size =
|caption =
|birth_date = {{birth date|df=yes|1905|5|8}}
|birth_place = Ambergate, England
|death_date = {{death date|df=yes|1979|10|}}
|death_place = London, England
|residence =
|citizenship =
|nationality = English
|ethnicity =
|field = Mathematics, Numerical integration, Functional analysis
|work_institutions =
|alma_mater = Newnham College, Cambridge
|doctoral_advisor =
|doctoral_students =
|known_for =
|author_abbrev_bot =
|author_abbrev_zoo =
|influences = Lancelot Stephen Bosanquet
|influenced =
|prizes =
|religion =
|signature =
}}
Winifred Lydia Caunden Sargent (8 May 1905 – October 1979) was an English mathematician. She studied at Newnham College, Cambridge and carried out research into Lebesgue integration, fractional integration and differentiation and the properties of BK-spaces.
Early life
Sargent was born into a Quaker family, daughter of Henry Sargent and Edith, his second wife, growing up in Fritchley, Derbyshire. She attended Ackworth School, a private school for Quakers, from 1915 to 1919. She then won a scholarship to attend The Mount School, York, another Quaker school, and later the Herbert Strutt School. In 1923, while there, she won a Derby scholarship, a State Scholarship, and a Mary Ewart scholarship to attend Newnham College, Cambridge and study mathematics in 1924.
While at Newnham she won further awards: an Arthur Hugh Clough Scholarship in 1927, a Mary Ewart Travelling Scholarship and a Goldsmiths Company Senior Studentship both in 1928. She graduated with a First class degree and remained at Cambridge conducting research but was unsatisfied by her progress and left to teach mathematics at Bolton High School.
Academic career
Sargent's first publication was in 1929, On Young's criteria for the convergence of Fourier series and their conjugates, published in the Mathematical Proceedings of the Cambridge Philosophical Society. In 1931 she was appointed an Assistant Lecturer at Westfield College and became a member of the London Mathematical Society in January 1932.[1] in 1936 she moved to Royal Holloway, University of London, at the time both women's colleges. In 1939 she became a doctoral student of Lancelot Bosanquet, but World War II broke out, preventing his formal supervision from continuing. In 1941 Sargent was promoted to lecturer at Royal Holloway, moving to Bedford College in 1948. She served on the Mathematical Association teaching committee from 1950 to 1954.[2] In 1954 she was awarded the degree of Sc.D. (Doctor of Science) by Cambridge and was given the title of Reader. While at the University of London she supervised Alan J. White in 1959.[3][4]
Bosanquet started a weekly seminar in mathematics in 1947, which Sargent attended without absence for twenty years until her retirement in 1967. She rarely presented at it, and did not attend mathematical conferences, despite being a compelling speaker.
Mathematical results
Much of Sargent's mathematical research involved studying types of integral, building on work done on Lebesgue integration and the Riemann integral. She produced results relating to the Perron and Denjoy integrals and Cesàro summation. Her final three papers consider BK-spaces or Banach coordinate spaces, proving a number of interesting results.[5]
For example, her 1936 paper[6] proves a version of Rolle's theorem for Denjoy–Perron integrable functions using different techniques from the standard proofs:[7] {{Quote|as in much of Dr. Sargent's work, the arguments are pushed as far as they will go and counter examples given to show that the results are the best possible.}}
Her 1953 paper[8] established several important results on summability kernels and is referenced in two textbooks on functional analysis.[9] Her papers in 1950 and 1957 contributed to fractional integration and differentiation theory.[10]
In her obituary, her work is described as being:[11]
{{Quote|marked by its exceptional lucidity, its exactness of expression and by the decisiveness of her results. She made important contributions to a field in which the complexity of the structure can only be revealed by subtle arguments.}}Papers
- {{cite journal
|title=On Young's criteria for the convergence of Fourier series and their conjugates
|last=Sargent
|first=Miss W. L. C.
|date=1929
|journal=Mathematical Proceedings of the Cambridge Philosophical Society
|volume=25
|issue=1
|pages=26–30
|doi = 10.1017/S030500410001851X| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
|ref = harv
- {{cite journal
|title = The Borel derivates of a function
|last = Sargent
|first = W. L. C.
|date = 1935
|journal = Proceedings of the London Mathematical Society
|doi = 10.1112/plms/s2-38.1.180
|series=Second Series
|issue = 1
|volume = 38
|pages = 180–196
|ref = harv}}
- {{cite journal
|title=On the Cesàro derivates of a function
|last=Sargent
|first=W. L. C.
|date=1936
|journal=Proceedings of the London Mathematical Society
|series=Second Series
|volume=40
|issue=1
|pages=235–254
|doi = 10.1112/plms/s2-40.1.235| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
|ref = harv
- {{cite journal
|title=A descriptive definition of Cesàro–Perron integrals
|last=Sargent
|first=W. L. C.
|date=1942a
|journal=Proceedings of the London Mathematical Society
|series=Second Series
|volume=47
|issue=1
|pages=212–247
|ref = harv
|doi = 10.1112/plms/s2-47.1.212| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On sufficient conditions for a function integrable in the Cesàro–Perron sense to be monotonic
|last=Sargent
|first=W. L. C.
|date=1942b
|journal=The Quarterly Journal of Mathematics
|series=Oxford Series
|volume=12
|issue=1
|pages=148–153
|ref = harv
|doi = 10.1093/qmath/os-12.1.148| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On the order of magnitude of the Fourier coefficients of a function integrable in the C{{sub|λ}}L sense
|last=Sargent
|first=W. L. C.
|date=1946a
|journal=Journal of the London Mathematical Society
|series=First Series
|volume=21
|issue=3
|pages=198–203
|ref = harv
|doi = 10.1112/jlms/s1-21.3.198| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=A mean value theorem involving Cesàro means
|last=Sargent
|first=W. L. C.
|date=1946b
|journal=Proceedings of the London Mathematical Society
|series=Second Series
|volume=49
|issue=1
|pages=227–240
|ref = harv
|doi = 10.1112/plms/s2-49.3.227| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On the integrability of a product
|last=Sargent
|first=W. L. C.
|date=1948a
|journal=Journal of the London Mathematical Society
|series=First Series
|volume=23
|issue=1
|pages=28–34
|ref = harv
|doi = 10.1112/jlms/s1-23.1.28| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On the summability (C) of allied series and the existence of
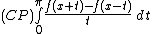
|last=Sargent
|first=W. L. C.
|date=1948b
|journal=Proceedings of the London Mathematical Society
|series=Second Series
|volume=50
|issue=1
|pages=330–348
|ref = harv
|doi = 10.1112/plms/s2-50.5.330| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On fractional integrals of a function integrable in the Cesàro-Perron sense
|last=Sargent
|first=W. L. C.
|date=1949
|journal=Proceedings of the London Mathematical Society
|series=Second Series
|volume=51
|issue=1
|pages=46–80
|ref = harv
|doi = 10.1112/plms/s2-51.1.46| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On linear functionals in spaces of conditionally integrable functions
|last=Sargent
|first=W. L. C.
|date=1950a
|journal=The Quarterly Journal of Mathematics
|series=Oxford Second Series
|volume=1
|issue=1
|pages=288–298
|ref = harv
|doi = 10.1093/qmath/1.1.288| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On the continuity (C) and integrability (CP) of fractional integrals
|last=Sargent
|first=W. L. C.
|date=1950b
|journal=Proceedings of the London Mathematical Society
|series=Second Series
|volume=52
|issue=1
|pages=253–270
|ref = harv
|doi = 10.1112/plms/s2-52.4.253| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On generalized derivatives and Cesàro–Denjoy integrals
|last=Sargent
|first=W. L. C.
|date=1950c
|journal=Proceedings of the London Mathematical Society
|series=Second Series
|volume=52
|issue=1
|ref = harv
|pages=365–376
|doi = 10.1112/plms/s2-52.5.365| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=Some properties of C{{sub|λ}}-continuous functions
|last=Sargent
|first=W. L. C.
|date=1951a
|journal=Journal of the London Mathematical Society
|series=First Series
|volume=26
|issue=2
|pages=116–121
|ref = harv
|doi = 10.1112/jlms/s1-26.2.116| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On the integrability of a product (II)
|last=Sargent
|first=W. L. C.
|date=1951b
|journal=Journal of the London Mathematical Society
|series=First Series
|volume=26
|issue=4
|pages=278–285
|ref = harv
|doi = 10.1112/jlms/s1-26.4.278| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=2213. On the differentiation of a function of a function
|last=Sargent
|first=W. L. C.
|date=1951c
|journal=The Mathematical Gazette
|volume=35
|number=312
|pages=121–122
|ref = harv
|doi = 10.2307/3609346| bibcode = | oclc =| id = | jstor = 3609346| language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On the summability of infinite integrals
|last=Sargent
|first=W. L. C.
|date=1952a
|journal=Journal of the London Mathematical Society
|series=First Series
|volume=27
|issue=4
|pages=401–413
|ref = harv
|doi = 10.1112/jlms/s1-27.4.401| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=Book review: Éléments de Mathématiques. XII by N. Bourbaki
|last=Sargent
|first=W. L. C.
|date=1952b
|journal=The Mathematical Gazette
|volume=36
|number=317
|pages=216–217
|ref = harv
|doi = 10.2307/3608266| bibcode = | oclc =| id = | jstor = 3608266| language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=Book review: Vorlesungen über Fouriersche Integrale by S. Bochner
|last=Sargent
|first=W. L. C.
|date=1952b
|journal=The Mathematical Gazette
|volume=36
|number=317
|pages=217–218
|ref = harv
|doi = 10.2307/3608268| bibcode = | oclc =| id = | jstor = 3608268| language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On some theorems of Hahn, Banach and Steinhaus
|last=Sargent
|first=W. L. C.
|date=1953
|journal=Journal of the London Mathematical Society
|series=First Series
|volume=28
|issue=4
|pages=438–451
|ref = harv
|doi = 10.1112/jlms/s1-28.4.438| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=Book review: Volume and Integral by W. W. Rogosinski
|last=Sargent
|first=W. L. C.
|date=1954
|journal=The Mathematical Gazette
|volume=38
|number=323
|page=67
|ref = harv
|doi = 10.2307/3609800| bibcode = | oclc =| id = | jstor = 3609800| language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On the transform

|last=Sargent
|first=W. L. C.
|date=1955
|journal=Journal of the London Mathematical Society
|series=First Series
|volume=30
|issue=4
|ref = harv
|pages=401–416
|doi = 10.1112/jlms/s1-30.4.401| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=Some summability factor theorems for infinite integrals
|last=Sargent
|first=W. L. C.
|date=1957a
|journal=Journal of the London Mathematical Society
|series=First Series
|volume=32
|issue=4
|pages=387–396
|ref = harv
|doi = 10.1112/jlms/s1-32.4.387| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On some cases of distinction between integrals and series
|last=Sargent
|first=W. L. C.
|date=1957b
|journal=Proceedings of the London Mathematical Society
|series=Third Series
|volume=7
|issue=1
|pages=249–264
|ref = harv
|doi = 10.1112/plms/s3-7.1.249| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=Some sequence spaces related to the l{{sub|p}} spaces
|last=Sargent
|first=W. L. C.
|date=1960
|journal=Journal of the London Mathematical Society
|series=First Series
|volume=35
|issue=2
|ref = harv
|pages=161–171
|doi = 10.1112/jlms/s1-35.2.161| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=Some analogues and extensions of Marcinkiewicz's interpolation problem
|last=Sargent
|first=W. L. C.
|date=1961
|journal=Proceedings of the London Mathematical Society
|series=Third Series
|volume=11
|issue=1
|pages=457–468
|ref = harv
|doi = 10.1112/plms/s3-11.1.457| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On sectionally bounded BK-spaces
|last=Sargent
|first=W. L. C.
|date=1964
|journal=Mathematische Zeitschrift
|volume=83
|issue=1
|pages=57–66
|ref = harv
|doi = 10.1007/BF01111108 | bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
- {{cite journal
|title=On compact matrix transformations between sectionally bounded BK-spaces
|last=Sargent
|first=W. L. C.
|date=1966
|journal=Journal of the London Mathematical Society
|series=First Series
|volume=41
|issue=1
|pages=79–87
|ref = harv
|doi = 10.1112/jlms/s1-41.1.79| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =
Notes
2. ^{{cite journal|title=Report of the Meeting of the Teaching Committee. 5th January 1950|date=1950|journal=The Mathematical Gazette|volume=34|issue=307|pages=5–7|doi = | bibcode = | oclc =| id = | jstor = 3610867| language = | laysummary = | laysource = | laydate = | quote = }}, p. 6.
3. ^{{Harvnb|White|1961|p=319}}.
4. ^{{cite web|title=Alan J. White|url=http://genealogy.math.ndsu.nodak.edu/id.php?id=42619|website=Mathematics Genealogy Project|publisher=Department of Mathematics, North Dakota State University|accessdate=15 October 2015}}
5. ^{{Harvnb|Sargent|1961}}, {{Harvnb|Sargent|1964}}, {{Harvnb|Sargent|1966}}.
6. ^{{Harvnb|Sargent|1936|pp=239–240}}.
7. ^{{Harvnb|Eggleston|1981|pp=173–174}}.
8. ^{{Harvnb|Sargent|1953}}.
9. ^{{cite book|last1=Swartz|first1=Charles|title=An introduction to functional analysis|date=1992|publisher=CRC Press|isbn=978-0824786434|pages=102–104}} and {{cite book|last1=Orlicz|first1=Władysław|title=Linear functional analysis|date=1992|publisher=World Scientific Publishing|isbn=978-9810208530|page=125}}
10. ^{{Harvnb|Sargent|1950a}}, {{Harvnb|Sargent|1950b}} and {{Harvnb|Sargent|1957a}}.
11. ^{{Harvnb|Eggleston|1981|p=175}}.
References
- {{cite journal
|last=Dixon
|first=Prof. A. C.
|author-link=Alfred Cardew Dixon
|date=1932
|title=Records of proceedings at meetings. Session November, 1931–June, 1932
|journal=Journal of the London Mathematical Society
|series=First Series
|volume=7
|issue=2
|pages=81–82
|publisher= |doi = 10.1112/jlms/s1-7.2.81| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =|ref = harv}}
- {{cite journal
|last=Eggleston
|first=H.G.
|authorlink=
|date=1981
|title=Winifred L. C. Sargent
|journal=Bulletin of the London Mathematical Society
|volume=13
|issue=2
|pages=173–176
|publisher= |doi = 10.1112/blms/13.2.173| bibcode = | oclc =| id = | url = | language = | laysummary = | laysource = | laydate = | quote =|ref = harv}}
- {{cite web|last1=O'Connor|first1=JJ|author-link1=John J. O'Connor (mathematician)|last2=Robertson|first2=EF|author-link2=Edmund F. Robertson|title=Winifred Lydia Caunden Sargent Biography|url=http://www-history.mcs.st-and.ac.uk/Biographies/Sargent.html|website=MacTutor History of Mathematics archive|publisher=University of St Andrews|accessdate=13 October 2015}}
- {{cite book|last1=Ogilvie|first1=Marilyn|author-link1=Marilyn Bailey Ogilvie|last2=Harvey|first2=Joy|title=The Biographical Dictionary of Women in Science: Pioneering Lives From Ancient Times to the Mid-20th Century |date=2000 |publisher=Routledge |isbn=978-0415920384 |pages=1152–1153 |url=https://books.google.co.uk/books?id=rUCUAgAAQBAJ&lpg=PT451&dq=winifred%20sargent&pg=PT451#v=onepage&q=winifred%20sargent&f=false}}
- {{cite journal|last1=White|first1=A. J.|title=On the restricted Cesàro summability of double Fourier series|journal=Transactions of the American Mathematical Society|date=1961|volume=99|issue=2|pages=308–319|doi=10.2307/1993402|ref = harv}}
- Wafangdian West Railway Station
- Wafaq ul Madaris Al-Arabia
- WAFA SC
- Wafa Shahenda
- Wafa (TV series)
- Wafayāt al-aʿyān wa-anbāʾ abnāʾ az-zamān
- WAFC-FM
- Wafda Saifan
- Wafda Saifan Lubis
- Wafer ash
- Waferdrive
- Wafer-level fan-out packaging
- Waffa
- Waffenbesitzkarte
- Waffenfarbe (Austria)
- Waffen-SS 13th division
- Waffen-SS historical revisionism
- Waffen-SS im Einsatz
- Waffen-SS in Action
- Waffen-SS in popular culture
- Waffen SS ranks
- Waffen-SS veterans in post-war Germany
- @WaffleHouse
- Wafflehouse shooting
- Waffle House shooting