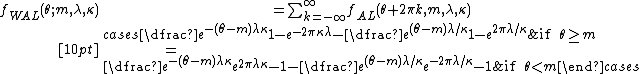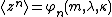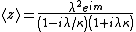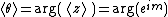- Definition
- Characteristic function
- Circular moments
- Generation of random variates
- See also
- References
name =Wrapped asymmetric Laplace distribution| type =density| pdf_image =
Wrapped asymmetric Laplace PDF with ''m'' = 0.Note that the ''κ'' = 2 and 1/2 curves are mirror images about θ=π | cdf_image =| parameters =location
 scale (real)
scale (real)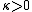 asymmetry (real) |
asymmetry (real) |
support =| pdf =(see article)| cdf =| mean =
(circular)| median =| mode =| variance =
(circular)| skewness =| kurtosis =| entropy =| mgf =| cf =
|
}}
In probability theory and directional statistics, a wrapped asymmetric Laplace distribution is a wrapped probability distribution that results from the "wrapping" of the asymmetric Laplace distribution around the unit circle. For the symmetric case (asymmetry parameter κ = 1), the distribution becomes a wrapped Laplace distribution. The distribution of the ratio of two circular variates (Z) from two different wrapped exponential distributions will have a wrapped asymmetric Laplace distribution. These distributions find application in stochastic modelling of financial data.
Definition
The probability density function of the wrapped asymmetric Laplace distribution is:[1]
where 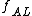 is the asymmetric Laplace distribution. The angular parameter is restricted to
is the asymmetric Laplace distribution. The angular parameter is restricted to  . The scale parameter is
. The scale parameter is  which is the scale parameter of the unwrapped distribution and
which is the scale parameter of the unwrapped distribution and 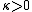 is the asymmetry parameter of the unwrapped distribution.
is the asymmetry parameter of the unwrapped distribution.
Characteristic function
The characteristic function of the wrapped asymmetric Laplace is just the characteristic function of the asymmetric Laplace function evaluated at integer arguments:
which yields an alternate expression for the wrapped asymmetric Laplace PDF in terms of the circular variable z=ei(θ-m) valid for all real θ and m:
where 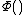 is the Lerch transcendent function and coth() is the hyperbolic cotangent function.
is the Lerch transcendent function and coth() is the hyperbolic cotangent function.
Circular moments
In terms of the circular variable  the circular moments of the wrapped asymmetric Laplace distribution are the characteristic function of the asymmetric Laplace distribution evaluated at integer arguments:
the circular moments of the wrapped asymmetric Laplace distribution are the characteristic function of the asymmetric Laplace distribution evaluated at integer arguments:
The first moment is then the average value of z, also known as the mean resultant, or mean resultant vector:
The mean angle is 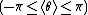
and the length of the mean resultant is
The circular variance is then 1 − R
Generation of random variates
If X is a random variate drawn from an asymmetric Laplace distribution (ALD), then  will be a circular variate drawn from the wrapped ALD, and,
will be a circular variate drawn from the wrapped ALD, and, 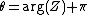 will be an angular variate drawn from the wrapped ALD with
will be an angular variate drawn from the wrapped ALD with 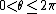 .
.
Since the ALD is the distribution of the difference of two variates drawn from the exponential distribution, it follows that if Z1 is drawn from a wrapped exponential distribution with mean m1 and rate λ/κ and Z2 is drawn from a wrapped exponential distribution with mean m2 and rate λκ, then Z1/Z2 will be a circular variate drawn from the wrapped ALD with parameters ( m1 - m2 , λ, κ) and 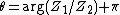 will be an angular variate drawn from that wrapped ALD with
will be an angular variate drawn from that wrapped ALD with 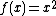 .
.
See also
- Wrapped distribution
- Directional statistics
References
- Senecio viscosus
- Senec, Rakovník
- Senec, Slovakia
- Senec (Slovakia)
- Senecú
- Sened
- Senedd
- Senedes
- Sene District
- Sened, Tunisia
- Senefelder, Aloys
- Senefelder Club
- Senefelderplatz (Berlin U-Bahn)
- Senega
- Senegal at the 1964 Summer Olympics
- Senegal at the 1968 Summer Olympics
- Senegal at the 1972 Summer Olympics
- Senegal at the 1976 Summer Olympics
- Senegal at the 1980 Summer Olympics
- Senegal at the 1984 Summer Olympics
- Senegal at the 1984 Winter Olympics
- Senegal at the 1988 Summer Olympics
- Senegal at the 1992 Summer Olympics
- Senegal at the 1992 Winter Olympics
- Senegal at the 1994 Winter Olympics