多元回归multiple regression

建立多个变量之间线性或非线性数学模型数量关系式的统计方法。在肥料试验中广泛应用。
多元线性回归 共N个处理的试验，每个处理有p个因素x₁,x₂，…，xp，取得N个观察值yα。如各因素x与观察值y的内在联系呈线性关系，观察值y可用多元线性数据结构式表示：

式(2)中β₀,β₁,β₂，…，β_p是p+1个待估参数，x₁、x₂、…，xp是p个可以测量或可控制的一般变量，在肥料试验中通常为各种肥料试验因素，ε_α是N个相互独立且服从正态分布N(0,σ)的随机变量。
式(1)的矩阵形式为：
Y=Xβ+ε. (3)
式(3)由以下四个向量和矩阵组成：

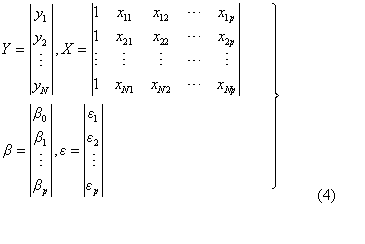
式(4)中矩阵X是多元线性回归模型的数据yα的结构矩阵，实际上是由各试验因素的水平所构成，亦即决定于试验设计方案。用最小二乘法可估出各项参数β，得回归方程为
ŷ=b₀+b₁x₁+b₂x₂+…+b_px_p (5)
参数b是由式(6)求得
b=(X′X)^-1X′Y=A^-1B=CB (6)
式(6)中：

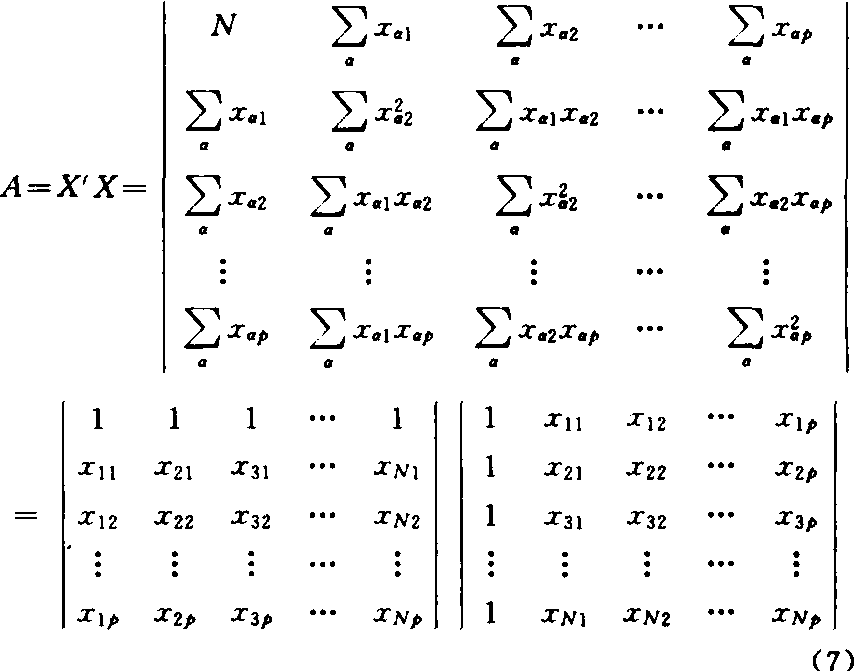
矩阵A是结构矩阵X的转置矩阵X′与该结构矩阵X的乘积，称为系数矩阵或信息矩阵。A^-1为A的逆矩阵C，称相关矩阵。

式(6)中B称为常数项矩阵，是结构矩阵X的转置矩阵X′与试验数据列向量Y的乘积。

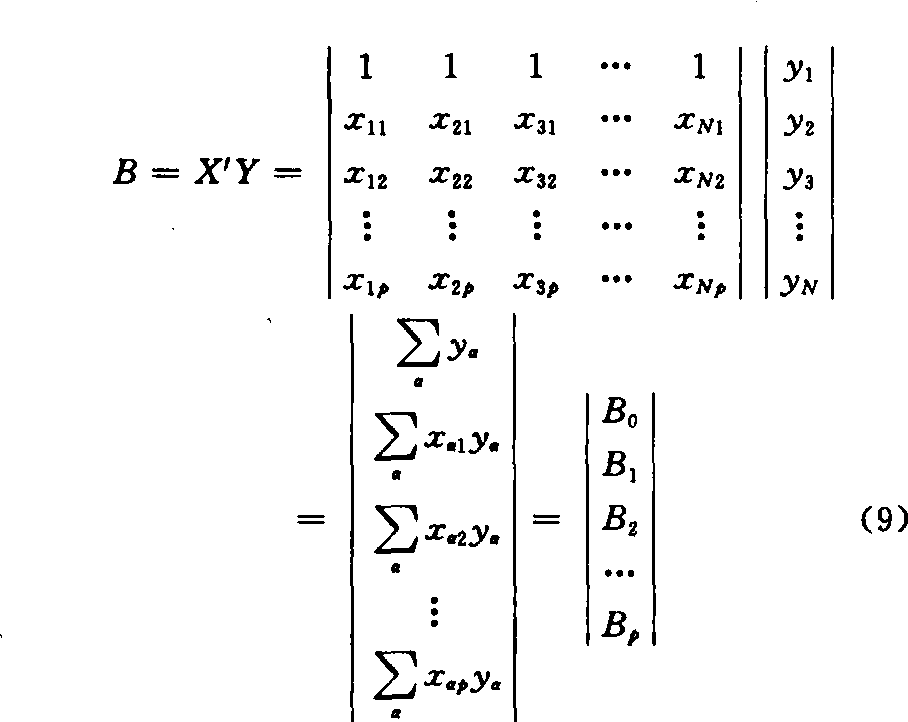
由式(6)，最小二乘估计b可用式(10)求得

b_k＝c_k0B₀+_ck1B₁+…+c_kpB_p (10)
k=1,2，…，p

式(10)中C_k0,C_k1，…，C_kp为相关矩阵C中各元素。
求出式(5)后尚需用方差分析法进行统计检验，将总平方和与总自由度分解为相应的回归与剩余两部分，然后进行F测验并假设各项回归系数等于零，即取无效假设H₀:β₁＝0,β₂＝0，…，β_p＝0。于是作F测验如表1所示：

表1 方差分析

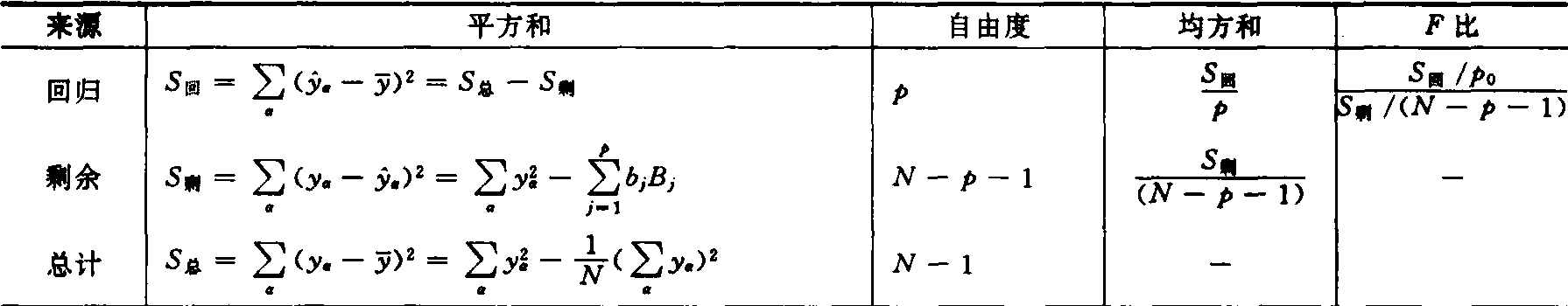
进行预报与控制。
逐步回归 式(5)经F测验只说明在一定概率水平下整个回归方程是否可靠，但不能说明其中某项因素是否显著。一个多元线性回归方程中如果包含不显著因素，在作预报时必须提供该因素的测定值，增加了不必要的工作量；不显著因素所提供的回归平方和较小，剩余平方和不会因此明显减小，而剩余自由度却有所减少，有时甚至导致剩余均方增大，从而影响整个回归方程的精度，于是产生了建立“最优”回归方程的需要，即包含所有对观察值y显著影响的因素，而影响不显著的因素不应包括在回归方程中。
建立“最优”回归方程的基本思路是先设置检验偏回归平方和的F测验显著标准，按照各因素x与观察值y相关系数的大小，将因素逐个引入。每引入一个新因素后，对已引入的因素的偏回归平方和进行检验，剔除不显著的因素。重复以上过程直至建立“最优”回归方程。由于计算过程较为繁复，通常在计算机上运行。
多项式回归 由于单因素施肥量与产量之间通常呈曲线关系，故常使用多项式回归来描述两者的关系，其回归模型为

正交多项式回归 多元线性回归及多项式回归的计算量随待估参数的数目增多而大量增加，而且各因素之间存在相关性。若需剔除不显著因素，则其他因素的回归系数需重新计算。解决这些困难的最常用办法是采用正交多项式，其前提是试验因素的水平间隔h要相等。对等间距水平的试验引进一族正交多项式，经数据变换后符合正交条件，从而消除了各因素之间相关性，并简化计算过程。正交多项式同样适用于多元多项式回归。
其他形式的多元非线性回归 除以上形式的多元非线性回归分析外，还有多种形式的多元非线性回归，只要取简单的数据变换形式，即可转化为多元线性回归，从求出各项待估参数，其主要形式列于表2。

表2 多元非线性回归线性化的方法