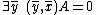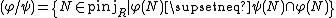“Ziegler spectrum”的意思、由来-开放百科全书

词条

Ziegler spectrum

释义

Definition
Properties
References

In mathematics, the (right) Ziegler spectrum of a ring R is a topological space whose points are (isomorphism classes of) indecomposable pure-injective right modules. Its closed subsets correspond to theories of modules closed under arbitrary products and direct summands. Ziegler spectra are named after Martin Ziegler, who first defined and studied them.^[1]

Definition

Let R be a ring. A (right) pp-n-formula is a formula in the language of (right) R-modules of the form

where 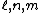are natural numbers, is an 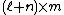matrix with entries from R, and 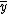is an -tuple of variables and 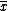is an -tuple of variables.

The (right) Ziegler spectrum, 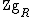, of R is the topological space whose points are isomorphism classes of indecomposable pure-injective right modules, denoted by 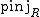; The topology

has the sets

as subbasis of open sets, where range over

(right) pp-1-formulae. One can show that these sets form a basis.

Properties

Ziegler spectra are rarely hausdorff and often fail to have the -property. However they are always compact and have a basis of compact open sets given by the sets 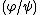where are pp-1-formulae.

When the ring R is countable 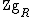is sober.^[2] It is not currently known if all Ziegler spectra are sober.

References

1. ^Martin Ziegler (1984). Model theory of modules. Ann. Pure Appl. Logic, 26:2 149–213
2. ^Ivo Herzog (1993). Elementary duality of modules. Trans. Amer. Math. Soc., 340:1 37–69

1 : Model theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。