多重比较multiple comparisions
多个互不独立的样本平均数间的成对比较。对包括k(k≥3)个样本(处理)的试验结果经F检验,否定了H0:μ1=μ2=…=μk,但这并不一定是所有样本平均数间都互不相等,可能其中若干个平均数是相等的。如果k=3,当F检验否定H0:μ1=μ2=μ3,则应接受的备择假设有如下4种可能:❶HA:μ1≠μ2≠μ3;
❷HA∶μ1≠μ2=μ3;
❸HA∶μ1=μ2≠μ3;
❹HA∶μ1=μ3≠μ2。多重比较可以对k个样本平均数所能组成的k×(k-1)÷2个成对比较作出差异显著性检验。常用方法有如下5种:
最小显著差数测验法 又称LSD法。即确定一个达到显著的最小差数尺度LSDα值,当任何两个样本平均数之差(i-j)的绝对值>LSDα,即为i与j在α水平上差异显著,反之,差异不显著。LSDα定义为
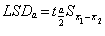

容量。LSD测验法实质上是t检验法。由于t检验法是用于检验两个随机样本平均数差异是否显著的方法。严格地说,LSD法只适用于比较一个阵列内相邻的平均数。或比较试验前已确定的彼此独立的处理平均数,例如,不同处理跟对照处理平均数的比较。
Dunnett最小差数法 一种专供测验若干个处理平均数i(i=1,2,…,k)与某一对照处理平均数0的差异显著性的多重比较方法,又称DLSD。当任一处理平均数i与0之差(i-0)的绝对值>DLSDα时,即为i与0在α水平上差异显著,DLSDα定义为
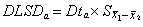


平均数之差xi-xj的显著性(i< j),由这两个平均数的秩次距(a=j-i+1)下的LSRa来判定,当|xi-xj|>LSRa为显著,否则不显著。LSRa定义为
LSRa=SSRa×Sx
式中 SSRa是保护水平P=(1-a)a-1,显著水平为a时,以平均数标准误为单位的标准化最短极差,随秩次距a和误差自由度而异。
学生氏复极差检验 简称q检验。其检验程序和新复极差法相同,但LSRa定义为LSRa=qa×Sx式中qa与Tukey固定极差法中的qa相同。在相同秩次距a下,qa比SSRa更为严格。
多重比较multiple comparisons
统计分析上,当方差分析的F测验表明处理间有显著差异时,进一步所进行的具体样本各平均数相互间的差异显著性比较。有最小显著差数法和最小显著极差法等。