069 大衍求一术

原为运用辗转相除求孙子剩余定理中各乘率的方法。现通指整数论中一次同余组的解法。设p₁,p₂……，p₁两两互素，M=p₁p₂…p₁，则同余式组x≡r_i(modp_i) (i=1,2，…，1)有整数解，且对模M唯一。其最小正整数解为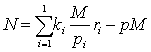，其中k_i满足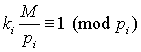(i=1,2，…，1)。整数p可适当选取，使N≤M。问题的关键是求得满足上述条件的k_i(i=1,2，…，1)。设p_s为p₁,p₂，…p₁中第s个数，先由M/p_s累减p_s，直到余数G

s，这时G≡M/p_s(mod p_s)。然后进行辗转相除，计算到余数r_n＝1时止。取当时相应的k_n为k_s. 同法求得k_i中的其余各数。求每个K_i，总要计算到余数等于1为止，“求一术”之名即缘于此。对于p₁,p₂，…p₁为非两两互素的整数及分数或小数的情况，秦九韶都给出了相应的处理方法。其思考周详，理论系统而严密，充分显示了秦九韶高超的数学水平和娴熟的计算技巧。大衍求一术是秦九韶最重要的数学成就，是他对中国传统数学的杰出贡献，也是世界数学宝库中一枝绚丽的奇葩。

大衍求一术

中国南宋数学家秦九韶所创立的一次同余组的解法。中国最早的见于记载的一次同余问题是所谓的“物不知数问题”(“孙子问题”):“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何”。写成现代的形式为：N=2(mod3)=3(mod5)=2(mod7)它等价于解不定方程组：N=3x+2,N=5y+3,N=7z+2，求正整数解N。秦九韶把它推广到一般，指出关键是求出一组称为“乘率”的数，其方法即是大衍求一术。他的解法简洁、明确，有很强的机械性。在今天，其程序可毫无困难地转化为算法语言，用计算机来求解。