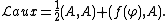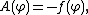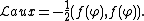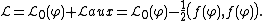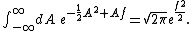“Auxiliary field”的意思、由来-开放百科全书

词条

Auxiliary field

释义

References

In physics, and especially quantum field theory, an auxiliary field is one whose equations of motion admit a single solution. Therefore, the Lagrangian describing such a field contains an algebraic quadratic term and an arbitrary linear term, while it contains no kinetic terms (derivatives of the field):

The equation of motion for is

and the Lagrangian becomes

Auxiliary fields do not propagate, and hence the content of any theory remains unchanged by adding such fields by hand.

If we have an initial Lagrangian 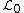describing a field , then the Lagrangian describing both fields is

Therefore, auxiliary fields can be employed to cancel quadratic terms in in 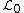and linearize the action .

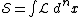Examples of auxiliary fields are the complex scalar field F in a chiral superfield, the real scalar field D in a vector superfield, the scalar field B in BRST and the field in the Hubbard–Stratonovich transformation.

The quantum mechanical effect of adding an auxiliary field is the same as the classical, since the path integral over such a field is Gaussian. To wit:

References

Superspace, or One thousand and one lessons in supersymmetry [https://arxiv.org/abs/hep-th/0108200 arXiv:hep-th/0108200]

1 : Quantum field theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。