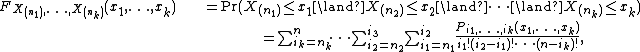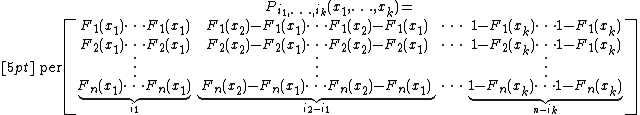“Bapat–Beg theorem”的意思、由来-开放百科全书

In probability theory, the Bapat–Beg theorem gives the joint probability distribution of order statistics of independent but not necessarily identically distributed random variables in terms of the cumulative distribution functions of the random variables. Ravindra Bapat and Beg published the theorem in 1989,^[1] though they did not offer a proof. A simple proof was offered by Hande in 1994.^[2]

Often, all elements of the sample are obtained from the same population and thus have the same probability distribution. The Bapat–Beg theorem describes the order statistics when each element of the sample is obtained from a different statistical population and therefore has its own probability distribution.^[1]

Statement of theorem

Let

be independent real valued random variables with cumulative distribution functions respectively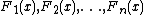

. Write

for the order statistics. Then the joint probability distribution of the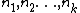

order statistics (with

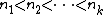and

) is

is the permanent of the given block matrix. (The figures under the braces show the number of columns.)^[1]

Independent identically distributed case

In the case when the variables

are independent and identically distributed with cumulative probability distribution function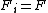

for all i the theorem reduces to

Remarks

Complexity

Glueck et al. note that the Bapat–Beg "formula is computationally intractable, because it involves an exponential number of permanents of the size of the number of random variables"^[3] However, when the random variables have only two possible distributions, the complexity can be reduced to O(m^2k).^[3] Thus, in the case of two populations, the complexity is polynomial in m for any fixed number of statistics k.

References

1. ^¹²³{{cite journal | first1= R. B. |last1=Bapat | first2= M. I. |last2= Beg | year = 1989 | title = Order Statistics for Nonidentically Distributed Variables and Permanents | journal = Sankhyā: The Indian Journal of Statistics, Series A (1961–2002) | volume = 51 | issue = 1 | pages = 79–93 | jstor = 25050725 | mr = 1065561}}
2. ^¹{{cite journal | first1= Sayaji | last1= Hande | year = 1994 | title = A Note on Order Statistics for Nondentically Distributed Variables | journal = Sankhyā: The Indian Journal of Statistics, Series A (1961–2002) | volume = 56 | issue = 2 | pages = 365–368 | jstor = 25050995 | mr = 1664921}}
3. ^¹{{cite journal|author1=Glueck|author2=Anis Karimpour-Fard|author3=Jan Mandel|author4=Larry Hunter|author5=Muller|title=Fast computation by block permanents of cumulative distribution functions of order statistics from several populations|doi=10.1080/03610920802001896|year=2008|journal=Communications in Statistics – Theory and Methods|volume=37|issue=18|pages=2815–2824|pmid=19865590|pmc=2768298|arxiv=0705.3851}}