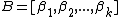“Base (group theory)”的意思、由来-开放百科全书

词条

Base (group theory)

释义

References

Let be a finite permutation group acting on a set . A sequence

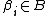of k distinct elements of is a base for G if the only element of which fixes every pointwise is the identity element of .^[1]

Bases and strong generating sets are concepts of importance in computational group theory. A base and a strong generating set (together often called a BSGS) for a group can be obtained using the Schreier–Sims algorithm.^[2]

It is often beneficial to deal with bases and strong generating sets as these may be easier to work with than the entire group. A group may have a small base compared to the set it acts on. In the "worst case", the symmetric groups and alternating groups have large bases (the symmetric group S_n has base size n − 1), and there are often specialized algorithms that deal with these cases.

References

1. ^{{citation|title=Permutation Groups|volume=163|series=Graduate Texts in Mathematics|first=John D.|last=Dixon|publisher=Springer|year=1996|isbn=9780387945996|page=76|url=https://books.google.com/books?id=4QDpFN6k61EC&pg=PA76}}.
2. ^{{citation|title=Permutation Group Algorithms|volume=152|series=Cambridge Tracts in Mathematics|first=Ákos|last=Seress|publisher=Cambridge University Press|year=2003|pages=1–2|isbn=9780521661034|url=https://books.google.com/books?id=hxFqdbfc_CMC&pg=PA1|quote=Sim's seminal idea was to introduce the notions of base and strong generating set}}.

2 : Permutation groups|Computational group theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。