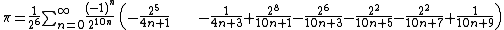“Bellard's formula”的意思、由来-开放百科全书

Bellard's formula was discovered by Fabrice Bellard in 1997. It is about 43% faster than the Bailey–Borwein–Plouffe formula.^[1] It has been used in PiHex, the now-completed distributed computing project.

One important application is verifying computations of all digits of pi performed by other means. Rather than having to compute all of the digits twice by two separate algorithms to ensure that a computation is correct, the final digits of a very long all-digits computation can be verified by the much faster Bellard's formula.^[2]

Formula

Notes

1. ^{{cite web|title=PiHex Credits|url=http://wayback.cecm.sfu.ca/projects/pihex/credits.html|website=Centre for Experimental and Constructive Mathematics|publisher=Simon Fraser University|accessdate=30 March 2018|archiveurl=https://web.archive.org/web/20170610094408/http://wayback.cecm.sfu.ca/projects/pihex/credits.html|archivedate=2017-06-10|dead-url=no|date=March 21, 1999}}
2. ^{{cite web |title=Hexadecimal Digits are Correct! |date=31 October 2016 |url=http://pi2e.ch/blog/2016/10/31/hexadecimal-digits-are-correct/ |first=Peter |last=Trueb |access-date=2016-12-28 |archiveurl=https://web.archive.org/web/20161116164638/http://pi2e.ch/blog/2016/10/31/hexadecimal-digits-are-correct/ |archivedate=2016-11-16 |dead-url=no}}

External links

Fabrice Bellard's PI page

[https://web.archive.org/web/20060804212241/http://oldweb.cecm.sfu.ca/projects/pihex/ PiHex web site]

David Bailey, Peter Borwein, and Simon Plouffe's BBP formula (On the rapid computation of various polylogarithmic constants) (PDF)

3 : Distributed computing projects|Pi algorithms|1997 introductions