存活曲线survivorship curve

种群个体在不同年龄阶段存活率（或存活数）的表达方式，也称生存曲线。将生命表中lx（存活数）、dx（死亡数）与qx（死亡率）的数值作成曲线，其中lx曲线特称存活曲线。存活曲线是建立预测预报模型的基础。
类型 存活曲线有多种类型。用相对年龄(即以平均寿命的百分比表示的年龄，记作x)作为横坐标，存活数lx的对数值作为纵坐标，绘成存活曲线图，以此比较不同寿命的动物。根据比较结果，珀尔(R. pe-arl) 1928年将存活曲线划分为A、B、C3种基本类型： A型，系呈凸形的存活曲线。表示种群在接近生理寿命之前，只有个别死亡，即几乎所有个体都能达到生理寿命。B型(指B₂) 系呈对角线型的存活曲线。表示各年龄期个体的死亡率大约相等，因此形成直线关系。C型系呈凹型的存活曲线。表示幼体死亡率很高，以后的死亡率低而稳定。1978年奥德姆(O. P. Odum)将B型又分为3种，共5型。昆虫多属C型和B3型，A型少见(图1)。斯洛博金(L.B.Slobodkin)1962年将存活曲线划分为4种基本类型(图2):❶凸线型：死亡主要发生在年老个体；
❷算术直线型：每个单位时间内死亡数为常数，即dx为常数，存活曲线呈算术型直线；
❸对数直线型：即死亡率qx为常数，存活曲线呈对数型直线；
❹凹线型：死亡主要发生在年幼阶段。

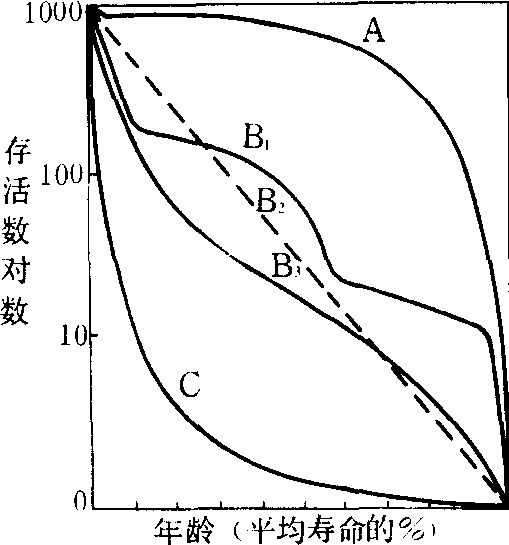
图 2 存活曲线类型之一
(仿E. S. Deevey)

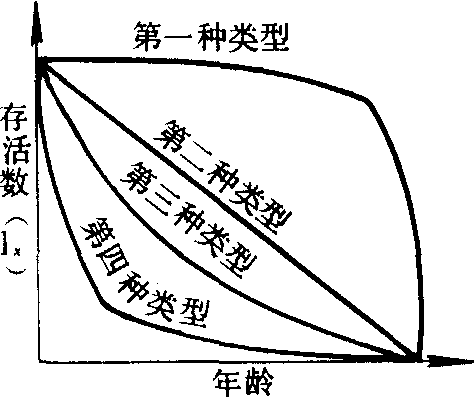
图2存活曲线类型之二 (仿L. B.Slobodkim.)

数学模型 由于造成种群死亡的作用因素不一，作用方式各异，因此应用数学方程表示这种复杂的函数关系时，应根据其具体方式考虑。若令s表示存活率，mi表示第i个因素作用下的死亡率(i=1、2、……n),x表示作用因素，则其数学模型可分为4类：❶若几个作用因素对害虫种群某虫态的作用同时进行，且作用相互独立，可用概率论计算积的理论表示这种净作用。设有两个因素进行作用，即为：

m=P(m_i)+P(m₂)-P(m_1m2)

其中m为害虫种群某虫态的总死亡率；P(m_i)为第1个因素造成的死亡概率。根据两件事都不发生的概率等于两个不发生概率之积的原理，则存活率为：

S=〔1-P(m₁)〕1-P(m₂)〕

❷若n个作用因素对害虫种群某虫态的作用是互不相交，则其总死亡率为n个死亡率之和：
m=P(m₁)+P(m₂)+……+P(m_n);S=1-P(m₁)+P(m₂)+……+P(m_n)〕

❸设有两个作用因素，若第二种因素致死作用的显著与否是依靠第一种因素的作用关系，这样在P(m₁)与P(m₂)之间即形成一函数关系。其存活率的数学方程为：

S=〔1-P(m₁)〕{1-f(P (m₁)〕}

❹若两个作用因素不同时发生，而是第二个因素紧随在第一个作用因素完成之后才开始起作用，其存活率的数学方程为：
S=1-P(m₁)-〔1-P(m1)〕P(m₂)