“Biholomorphism”的意思、由来-开放百科全书

词条

Biholomorphism

释义

Formal definition
Riemann mapping theorem and generalizations
Alternative definitions
References

In the mathematical theory of functions of one or more complex variables, and also in complex algebraic geometry, a biholomorphism or biholomorphic function is a bijective holomorphic function whose inverse is also holomorphic.

Formal definition

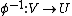Formally, a biholomorphic function is a function defined on an open subset U of the -dimensional complex space Cⁿ with values in Cⁿ which is holomorphic and one-to-one, such that its image is an open set in Cⁿ and the inverse is also holomorphic. More generally, U and V can be complex manifolds. As in the case of functions of a single complex variable, a sufficient condition for a holomorphic map to be biholomorphic onto its image is that the map is injective, in which case the inverse is also holomorphic (e.g., see Gunning 1990, Theorem I.11).

If there exists a biholomorphism 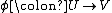, we say that U and V are biholomorphically equivalent or that they are biholomorphic.

Riemann mapping theorem and generalizations

If 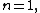every simply connected open set other than the whole complex plane is biholomorphic to the unit disc (this is the Riemann mapping theorem). The situation is very different in higher dimensions. For example, open unit balls and open unit polydiscs are not biholomorphically equivalent for 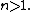In fact, there does not exist even a proper holomorphic function from one to the other.

Alternative definitions

In the case of maps f : U → C defined on an open subset U of the complex plane C, some authors (e.g., Freitag 2009, Definition IV.4.1) define a conformal map to be an injective map with nonzero derivative i.e., f’(z)≠ 0 for every z in U. According to this definition, a map f : U → C is conformal if and only if f: U → f(U) is biholomorphic. Other authors (e.g., Conway 1978) define a conformal map as one with nonzero derivative, without requiring that the map be injective. According to this weaker definition of conformality, a conformal map need not be biholomorphic even though it is locally biholomorphic. For example, if f: U → U is defined by f(z) = z² with U = C–{0}, then f is conformal on U, since its derivative f’(z) = 2z ≠ 0, but it is not biholomorphic, since it is 2-1.

References

{{cite book | author=John B. Conway | title=Functions of One Complex Variable | publisher=Springer-Verlag | year=1978 | isbn=3-540-90328-3 }}
{{cite book | author=John P. D'Angelo | title=Several Complex Variables and the Geometry of Real Hypersurfaces | publisher=CRC Press | year=1993 | isbn= 0-8493-8272-6}}
{{cite book | author=Eberhard Freitag and Rolf Busam | title=Complex Analysis | publisher=Springer-Verlag | year=2009 | isbn= 978-3-540-93982-5}}
{{cite book | author=Robert C. Gunning | title=Introduction to Holomorphic Functions of Several Variables, Vol. II | publisher=Wadsworth | year=1990 | isbn= 0-534-13309-6}}
{{cite book | author=Steven G. Krantz | title=Function Theory of Several Complex Variables | publisher=American Mathematical Society | year=2002 | isbn= 0-8218-2724-3}}

{{PlanetMath attribution|id=6032|title=biholomorphically equivalent}}

4 : Several complex variables|Algebraic geometry|Complex manifolds|Functions and mappings

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。