请输入您要查询的百科知识：

　

词条 BK-tree
释义

  1. See also

  2. References

  3. External links

{{technical|date=March 2019}}

A BK-tree is a metric tree suggested by Walter Austin Burkhard and Robert M. Keller{{ref|BK73}} specifically adapted to discrete metric spaces.

For simplicity, let us consider integer discrete metric . Then, BK-tree is defined in the following way. An arbitrary element a is selected as root node. The root node may have zero or more subtrees. The k-th subtree is recursively built of all elements b such that 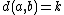. BK-trees can be used for approximate string matching in a dictionary {{ref|BN98}}.{{example needed|date=March 2019}}

See also

  • Levenshtein distance – the distance metric commonly used when building a BK-tree
  • Damerau–Levenshtein distance – a modified form of Levenshtein distance that allows transpositions

References

  • {{note|BK73}} W. Burkhard and R. Keller. Some approaches to best-match file searching, CACM, 1973
  • {{note|BCMW04}} R. Baeza-Yates, W. Cunto, U. Manber, and S. Wu. Proximity matching using fixed queries trees. In M. Crochemore and D. Gusfield, editors, 5th Combinatorial Pattern Matching, LNCS 807, pages 198–212, Asilomar, CA, June 1994.
  • {{note|BN98}} Ricardo Baeza-Yates and Gonzalo Navarro. Fast Approximate String Matching in a Dictionary. Proc. SPIRE'98

External links

  • A BK-tree implementation in [https://github.com/vy/bk-tree Common Lisp] with test results and performance graphs.
  • An explanation of BK-Trees and their relationship to metric spaces  
  • An explanation of BK-Trees with an implementation in C# 
  • A BK-tree implementation in Lua [https://profan.github.io/lua-bk-tree/]
{{CS-Trees}}{{datastructure-stub}}

1 : Trees (data structures)
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/13 18:58:46