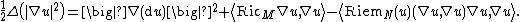- Statement of the result
- See also
- References
- External links
In mathematics — specifically, differential geometry — the Bochner identity is an identity concerning harmonic maps between Riemannian manifolds. The identity is named after the American mathematician Salomon Bochner.
Statement of the result
Let M and N be Riemannian manifolds and let u : M → N be a harmonic map. Let du denote the derivative (pushforward) of u, ∇ the gradient, Δ the Laplace–Beltrami operator, RiemN the Riemann curvature tensor on N and RicM the Ricci curvature tensor on M. Then
See also
- Bochner's formula
References
- {{cite journal
| last = Eells
| first = J
|author2=Lemaire, L.
| title = A report on harmonic maps
| journal = Bull. London Math. Soc.
| volume = 10
| year = 1978
| issue = 1
| pages = 1–68
| doi = 10.1112/blms/10.1.1
| mr = 495450
}}
External links
- {{MathWorld|urlname=BochnerIdentity|title=Bochner identity}}
2 : Differential geometry|Mathematical identities
- Not Tonight (Remix)
- Nottonville
- Not Too Amused
- Not Too Amused EP
- Not too late for love
- Not Too Much to Ask
- Not Too Sharp
- Not Too Young (album)
- Not Too Young (Album)
- Not Too Young (Mission Six album)
- Not Too Young (Mission Six Album)
- Not Too Young, Not Too Old
- Not to touch the earth
- Not to us
- Nottoway (disambiguation)
- Nottoway Indian Tribe
- Nottoway Plantation
- Nottoway Plantation House
- Nottoway Tribe
- Nottoway, VA
- Nottoway, Va
- Nott's County
- Notts County F C
- Notts County F. C.
- Notts County F.C. season 2008-09