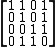请输入您要查询的百科知识：

　

词条 Bondy's theorem
释义

  1. Statement

  2. Example

  3. Learning theory application

  4. Notes

In mathematics, Bondy's theorem is a bound on the number of elements needed to distinguish the sets in a family of sets from each other. It belongs to the field of combinatorics, and is named after John Adrian Bondy, who published it in 1972.[1]

Statement

The theorem is as follows:

Let X be a set with n elements and let A1, A2, ..., An be distinct subsets of X. Then there exists a subset S of X with n − 1 elements such that the sets Ai ∩ S are all distinct.

In other words, if we have a 0-1 matrix with n rows and n columns such that each row is distinct, we can remove one column such that the rows of the resulting n × (n − 1) matrix are distinct.[2][3]

Example

Consider the 4 × 4 matrix

where all rows are pairwise distinct. If we delete, for example, the first column, the resulting matrix

no longer has this property: the first row is identical to the second row. Nevertheless, by Bondy's theorem we know that we can always find a column that can be deleted without introducing any identical rows. In this case, we can delete the third column: all rows of the 3 × 4 matrix

are distinct. Another possibility would have been deleting the fourth column.

Learning theory application

From the perspective of computational learning theory, Bondy's theorem can be rephrased as follows:[4]

Let C be a concept class over a finite domain X. Then there exists a subset S of X with the size at most |C| − 1 such that S is a witness set for every concept in C.

This implies that every finite concept class C has its teaching dimension bounded by |C| − 1.

Notes

1. ^{{Citation | last=Bondy | first=J. A. | authorlink=John Adrian Bondy | title=Induced subsets | journal=Journal of Combinatorial Theory, Series B | volume=12 | year=1972 | pages=201–202 | doi=10.1016/0095-8956(72)90025-1 | mr=0319773}}.
2. ^{{citation | first=Stasys | last=Jukna | title=Extremal Combinatorics with Applications in Computer Science | publisher=Springer | year=2001 | isbn=978-3-540-66313-3}}, Section 12.1.
3. ^{{citation | first1=Peter | last1=Clote | first2=Jeffrey B. | last2=Remmel | title=Feasible Mathematics II | publisher=Birkhäuser | year=1995 | isbn=978-3-7643-3675-2}}, Section 4.1.
4. ^{{citation | last1 = Kushilevitz | first1 = Eyal | last2 = Linial | first2 = Nathan | last3 = Rabinovich | first3 = Yuri | last4 = Saks | first4 = Michael | doi = 10.1016/S0097-3165(96)80015-X | issue = 2 | journal = Journal of Combinatorial Theory | mr = 1370141 | pages = 376–380 | series = Series A | title = Witness sets for families of binary vectors | volume = 73 | year = 1996}}.

2 : Computational learning theory|Theorems in combinatorics
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/11 13:37:17