一般二次方程的讨论yiban erci fangcheng de taolun
一般二元二次方程Ax2+Bxy+Cy2+Dx+Ey+F=0,只要根据△=B2-4AC的值为正、为负或为零,就可以直接判定它是双曲线型、椭圆型或抛物线型的曲线方程(详见下表).这些曲线都是圆锥截面所割成的曲线,所以二元二次方程所表示的曲线是圆锥曲线,并称二元二次方程为圆锥曲线方程,称△=B2-4AC为二元二次方程的判别式。
一个代数方程,通过移轴或转轴,它的次数是不变的,这是解析几何中的一条重要的性质。曲线是以方程的次数来区别的,因此也称直线为一次曲线,圆锥曲线为二次曲线,圆锥曲线的特例也叫退化圆锥曲线.
| 方程Ax2+Bxy+Cy2+Dx+Ey+F=0 | ||||
| 条 件 | 类 型 | 一般情况 | 特例(退化圆锥曲线) | |
| △≠0 (有心圆 锥曲线) | △<0 | 椭圆型 | 椭圆 | ❶点(点椭圆) ❷无轨迹(虚椭圆) |
| △>0 | 双曲线型 | 双曲线 | 两相交直线 | |
| △=0 (无心圆锥曲线) | 抛物线型 | 抛物线 | ❶两平行线 ❷一直线 (两条重合直线) ❸无轨迹 (两虚直线) | |
为了把一般二元二次方程变为标准型,需要移轴和转轴,这在计算上都比较繁。对于只具有数字系数的方程,比较简单的化简方法如下:
❶对于有心圆锥曲线方程可以先移轴后转轴。即以它的中心(h,k)为新原点,通过移轴消去x,y的一次项,得到形如Ax′2+Bx′y′+Cy′2+F′=0的方程,再转轴消去x′y′项,得到形如A′x″2+C′y″2+F′ =0的新方程.其中
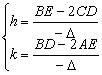
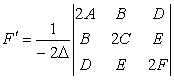
| 或 |
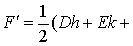
| 2F). |
第二步转轴时,可以不用转轴公式,而利用不变式建立方程组
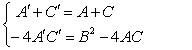
❷对于无心圆锥曲线的方程,一般是先转轴后移轴.即利用转轴消去它的xy项,再用配方法把方程化为抛物线型标准方程.
| 一般将原方程变为 |
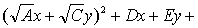 F=0的形式,再代入转轴公式化简比较简便.得到第一次的新方程A′x′2+D′x+E′y+F=0或C′y′2+D′x+E′y+F=0后,用配方法以移轴,化为抛物线的标准式A′x″2+E″y″=0或C′y″2+D″x″=0.
F=0的形式,再代入转轴公式化简比较简便.得到第一次的新方程A′x′2+D′x+E′y+F=0或C′y′2+D′x+E′y+F=0后,用配方法以移轴,化为抛物线的标准式A′x″2+E″y″=0或C′y″2+D″x″=0.关于特例,可以用分解因式或其它方法处理.