- Definition
- Recurrence relation
- As a sum
- The exponential generating function
- References
In mathematics, the boustrophedon transform is a procedure which maps one sequence to another. The transformed sequence is computed by filling a triangular array in boustrophedon (zig-zag) manner.
Definition
Given a sequence 
, the boustrophedon transform yields another sequence, 
, which is constructed by filling up a triangle as pictured on the right. Number the rows in the triangle starting from 0, and fill the rows consecutively. Let k denote the number of the row currently being filled.
If k is odd, then put the number 
on the right end of the row and fill the row from the right to the left, with every entry being the sum of the number to the right and the number to the upper right. If k is even, then put the number on the left end and fill the row from the left to the right, with every entry being the sum of the number to the left and the number to the upper left.
Defining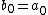 
, the numbers 
forming the transformed sequence can then be found on the left end of odd-numbered rows and on the right end of even-numbered rows, that is, opposite to the numbers .
Recurrence relation
A more formal definition uses a recurrence relation. Define the numbers 
(with k ≥ n ≥ 0) by
Then the transformed sequence is defined by 
.
In the case a0 = 1, an = 0 (n > 0), the resulting triangle is called the Seidel–Entringer–Arnold Triangle and the numbers are called Entringer numbers {{OEIS|id=A008281}}. In this case the numbers in the transformed sequence bn are called the Euler up/down numbers. This is sequence A000111 on the On-Line Encyclopedia of Integer Sequences. These enumerate the number of alternating permutations on n letters and are related to the Euler numbers and the Bernoulli numbers.
As a sum
The terms of a sequence {{math|(a{{sub|n}})}} and its boustrophedon transform {{math|(b{{sub|n}})}} are related by
where {{math|(E{{sub|n}})}} is the sequence of up/down numbers.
The exponential generating function
The exponential generating function of a sequence (an) is defined by
The exponential generating function of the boustrophedon transform (bn) is related to that of the original sequence (an) by
The exponential generating function of the unit sequence is 1, so that of the up/down numbers is sec x + tan x.
References
- Jessica Millar, N.J.A. Sloane, Neal E. Young, "A New Operation on Sequences: the Boustrouphedon Transform," Journal of Combinatorial Theory, Series A, volume 76, number 1, pages 44–54, 1996. Also available in a slightly different version as e-print [https://arxiv.org/abs/math.CO/0205218 math.CO/0205218] on the arXiv.
- {{cite book |author=Weisstein, Eric W. |title=CRC Concise Encyclopedia of Mathematics, Second Edition |publisher=Chapman & Hall/CRC |year=2002 |page=273 |isbn=1-58488-347-2}}