定积分dingjffen
是积分学的基本概念之一. 设函数f (x)在区间 [a,b]上有定义,用分点
a = x0
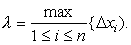 在每一个小区间[xi-1,xi]上任取一点ξi,并且作和
在每一个小区间[xi-1,xi]上任取一点ξi,并且作和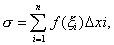 这个和称为函数f (x)在区间 [a,b ]上的积分和.若当λ→0时,不管区间[a,b]的分法如何,也不管ξ的取法如何,和数σ存在极限I,即
这个和称为函数f (x)在区间 [a,b ]上的积分和.若当λ→0时,不管区间[a,b]的分法如何,也不管ξ的取法如何,和数σ存在极限I,即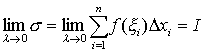
则称极限值I为函数f (x)在区间[a,b]上的定积分记作
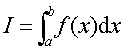
定积分的定义也可用ε—δ语言来表述.设f(x)是定义在区间[a,b]上的一个函数,I是一个确定的数.
若对任给的正数ε,总存在一个正数δ,使得对于区间[a,b]分成n个小区间 [xi-1,xi]的任意分法,只要
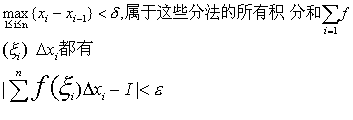 属于这些分法的所有积分和
属于这些分法的所有积分和 (ζi) △xi都有
(ζi) △xi都有![]()
这个定义是法国数学家B.黎曼首先给出的,所以这个意义下的定积分通常称为黎曼积分.
极限
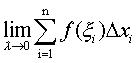 不同于数列极限和函数极限. 当λ→0时,对于λ=max {△xi}的每个值,一般都有无穷多个积分和与它对应,因此,这种极限比数列极限和函数极限复杂. 尽管如此,可积函数的积分和仍保持着与数列极限及函数极限在本质上的相同之处,即当λ→0时,积分和无限接近常数I. 因此,可积函数的积分和有一系列与函数极限类似的性质.
不同于数列极限和函数极限. 当λ→0时,对于λ=max {△xi}的每个值,一般都有无穷多个积分和与它对应,因此,这种极限比数列极限和函数极限复杂. 尽管如此,可积函数的积分和仍保持着与数列极限及函数极限在本质上的相同之处,即当λ→0时,积分和无限接近常数I. 因此,可积函数的积分和有一系列与函数极限类似的性质.定积分的概念来源于几何、物理和其他学科中的一类实际问题. 例如,求某个曲边梯形的面积; 求作变速运动的质点在某一段时间内走过的路程等等. 这类问题的共性是: ❶所求的量都是在某个区间上变化不均匀的整体量;
❷处理这类问题的方法是,先将整体量分为局部量,并求出各局部量的近似值,再求和,以求得整体量的近似值,最后在无限细分的极限过程中求出整体量的精确值. 经过对上述基本思想的概括和抽象,人们建立了定积分的概念.
中学教材中介绍的定积分概念,是定积分的特殊情形. 这种特殊性表现在❶仅就连续函数建立定积分概念. 由于连续函数在闭区间上必可积,因而其和数极限必存在,所以在教材的定义中,直接肯定了和数极限的存在性.
❷在肯定了和数极限存在的前提下,考虑用等分法分割区间 [a,b],于是λ→0便等价于n→∞. 这种特殊的处理方法比较简明易懂,而又不失定积分的基本特征,所以,教材这种安排将有助于学生掌握初等微积分的定积分知识。
定积分
设函数f(x)是[a,b]上的有界函数,对[a,b]进行任意分割得a0=x0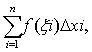 当最大的△xi趋于零且分点无穷多时,上述和式的极限存在,就称此极限值为f(x)在[a,b]上的定积分,记为
当最大的△xi趋于零且分点无穷多时,上述和式的极限存在,就称此极限值为f(x)在[a,b]上的定积分,记为 f(x)dx。如果考虑取函数为二元以上的函数f(x1 ,…,xn)(n=2,3,…,N),类似定积分对自变量的区域进行任意分割,作和,取极限,若极限存在,便称此极限值为f(x1,…,xn)的n重定积分,记为
f(x)dx。如果考虑取函数为二元以上的函数f(x1 ,…,xn)(n=2,3,…,N),类似定积分对自变量的区域进行任意分割,作和,取极限,若极限存在,便称此极限值为f(x1,…,xn)的n重定积分,记为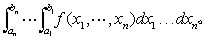 定积分在物理、工程技术等许多领域都有广泛的应用。
定积分在物理、工程技术等许多领域都有广泛的应用。