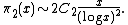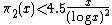- Asymptotic bounds on twin primes
- Numerical estimates
- Further results In popular culture
- See also
- Notes
- References
- External links
In number theory, Brun's theorem states that the sum of the reciprocals of the twin primes (pairs of prime numbers which differ by 2) converges to a finite value known as Brun's constant, usually denoted by B2 {{OEIS|id=A065421}}. Brun's theorem was proved by Viggo Brun in 1919, and it has historical importance in the introduction of sieve methods.
Asymptotic bounds on twin primes
The convergence of the sum of reciprocals of twin primes follows from bounds on the density of the sequence of twin primes.
Let  denote the number of primes p ≤ x for which p + 2 is also prime (i.e.
denote the number of primes p ≤ x for which p + 2 is also prime (i.e.  is the number of twin primes with the smaller at most x). Then, for x ≥ 3, we have
is the number of twin primes with the smaller at most x). Then, for x ≥ 3, we have
That is, twin primes are less frequent than prime numbers by nearly a logarithmic factor.
It follows from this bound that the sum of the reciprocals of the twin primes converges, or stated in other words, the twin primes form a small set. In explicit terms the sum
either has finitely many terms or has infinitely many terms but is convergent: its value is known as Brun's constant.
The fact that the sum of the reciprocals of the prime numbers diverges implies that there are infinitely many prime numbers. Because the sum of the reciprocals of the twin primes instead converges, it is not possible to conclude from this result that there are finitely many or infinitely many twin primes. Brun's constant could be an irrational number only if there are infinitely many twin primes.
Numerical estimates
The series converges extremely slowly. Thomas Nicely remarks that after summing the first one billion (109) terms, the relative error is still more than 5%.[1].
By calculating the twin primes up to 1014 (and discovering the Pentium FDIV bug along the way), Nicely heuristically estimated Brun's constant to be 1.902160578.[2] Nicely has extended his computation to 1.6{{e|15}} as of 18 January 2010 but this is not the largest computation of its type.
In 2002, Pascal Sebah and Patrick Demichel used all twin primes up to 1016 to give the estimate:[3]
B2 ≈ 1.902160583104.
It is based on extrapolation from the sum 1.830484424658... for the twin primes below 1016. Dominic Klyve showed conditionally (in an unpublished thesis) that B2 < 2.1754 (assuming the extended Riemann hypothesis). It has been shown unconditionally that B2 < 2.347.[4]
There is also a Brun's constant for prime quadruplets. A prime quadruplet is a pair of two twin prime pairs, separated by a distance of 4 (the smallest possible distance). The first prime quadruplets are (5, 7, 11, 13), (11, 13, 17, 19), (101, 103, 107, 109). Brun's constant for prime quadruplets, denoted by B4, is the sum of the reciprocals of all prime quadruplets:
with value:
B4 = 0.87058 83800 ± 0.00000 00005, the error range having a 99% confidence level according to Nicely.[5]
This constant should not be confused with the Brun's constant for cousin primes, as prime pairs of the form (p, p + 4), which is also written as B4. Wolf derived an estimate for the Brun-type sums Bn of 4/n.
Further results
Let 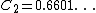 {{OEIS|A005597}} be the twin prime constant. Then it is conjectured that
{{OEIS|A005597}} be the twin prime constant. Then it is conjectured that
In particular,
for every  and all sufficiently large x.
and all sufficiently large x.
Many special cases of the above have been proved. Most recently, Jie Wu proved that for sufficiently large x,
where 4.5 corresponds to  in the above.
in the above.
In popular culture
The digits of Brun's constant were used in a bid of $1,902,160,540 in the Nortel patent auction. The bid was posted by Google and was one of three Google bids based on mathematical constants.[6]
See also
- Divergence of the sum of the reciprocals of the primes
- Meissel–Mertens constant
Notes
2. ^{{cite web |url=http://www.trnicely.net/twins/twins2.html |last=Nicely |first=Thomas R. |title=Enumeration to 1.6*10^15 of the twin primes and Brun's constant |accessdate=16 February 2010 |work=Some Results of Computational Research in Prime Numbers (Computational Number Theory) |date=18 January 2010}}
3. ^{{cite web | url=http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.464.1118&rep=rep1&type=pdf | last1=Sebah | first1=Pascal | last2=Gourdon | first2=Xavier | title=Introduction to twin primes and Brun’s constant computation | access-date=5 January 2018}}
4. ^{{cite web |url=http://libarchive.dartmouth.edu/cdm/ref/collection/dcdis/id/36604 |last=Klyve |first=Dominic |title=Explicit bounds on twin primes and Brun's Constant |accessdate=13 May 2015}}
5. ^{{cite web |url=http://www.trnicely.net/quads/quads.html |last=Nicely |first=Thomas R. |title=Enumeration to 1.6{{e|15}} of the prime quadruplets |accessdate=9 March 2009 |work=Some Results of Computational Research in Prime Numbers (Computational Number Theory) |date=26 August 2008}}
6. ^{{cite web | url=https://www.reuters.com/article/2011/07/02/us-dealtalk-nortel-google-idUSTRE76104L20110702 | title=Dealtalk: Google bid "pi" for Nortel patents and lost | publisher=Reuters | date=1 July 2011 | accessdate=6 July 2011 | author=Damouni, Nadia}}
References
{{refbegin}}- {{cite journal | first=Viggo|last= Brun | authorlink=Viggo Brun | title=Über das Goldbachsche Gesetz und die Anzahl der Primzahlpaare | journal=Archiv for Mathematik og Naturvidenskab | volume=B34 | issue=8 | year=1915 }}
- {{cite journal|language=French| first=Viggo|last= Brun | authorlink=Viggo Brun | title=La série 1/5+1/7+1/11+1/13+1/17+1/19+1/29+1/31+1/41+1/43+1/59+1/61+..., où les dénominateurs sont nombres premiers jumeaux est convergente ou finie | url=http://gallica.bnf.fr/ark:/12148/bpt6k486270d |journal=Bulletin des Sciences Mathématiques | year=1919 | volume=43 | pages=100–104, 124–128 }}
- {{cite book | first1=Alina Carmen|last1= Cojocaru|author1-link= Alina Carmen Cojocaru | first2=M. Ram|last2= Murty |author2-link=M. Ram Murty| title=An introduction to sieve methods and their applications | series=London Mathematical Society Student Texts | volume=66 | publisher=Cambridge University Press | isbn=0-521-61275-6 | pages=73–74 | year=2005 }}
- {{cite book | first=E.|last=Landau | authorlink=Edmund Landau | title=Elementare Zahlentheorie | location=Leipzig, Germany | publisher=Hirzel | year=1927}} Reprinted Providence, RI: Amer. Math. Soc., 1990.
- {{cite book | first=William Judson|last= LeVeque |authorlink=William J. LeVeque| title=Fundamentals of Number Theory | location=New York City| publisher=Dover Publishing | year=1996 | pages=1–288 | isbn=0-486-68906-9}} Contains a more modern proof.
- {{cite journal |first=J. |last= Wu |title=Chen's double sieve, Goldbach's conjecture and the twin prime problem |journal= Acta Arithmetica |volume=114 |pages=215–273 |year=2004 |origyear=24 Sep 2007 |issue=3 |doi= 10.4064/aa114-3-2 |arxiv= 0705.1652|bibcode=2004AcAri.114..215W }}
External links
- {{mathworld|urlname=BrunsConstant|title=Brun's Constant}}
- {{mathworld|urlname=BrunsTheorem|title=Brun's Theorem}}
- {{PlanetMath|urlname=BrunsConstant|title=Brun's constant}}
- Sebah, Pascal and Xavier Gourdon, Introduction to twin primes and Brun's constant computation, 2002. A modern detailed examination.
- [https://web.archive.org/web/20110109082911/http://www.ift.uni.wroc.pl/~mwolf/ Wolf's article on Brun-type sums]
- Rida Khawaldeh
- Rida Young
- Ridaz
- Ridaz (Eminem song)
- Riddah wars
- Riddar Tynne
- Riddarvisa
- Riddell (disambiguation)
- Riddell, George
- Riddell, Maria
- Riddell, Mark
- Riddell, Richard
- Riddell's goldenrod
- Riddell Sports Group, Inc.
- Riddell, Victor
- Riddell-Webster, Michael
- Riddell-Webster, Thomas
- Riddell, William
- Riddelsdell
- Ridder af Elefantordenen
- Ridderhof Mall shooting
- Ridderhof, Mark
- Ridderwall, Stefan
- Riddet, William
- Riddhi Dogra