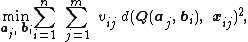“Bundle adjustment”的意思、由来-开放百科全书

词条

Bundle adjustment

释义

Uses
General approach
Mathematical definition
Software
See also
References
Further reading

Uses

Bundle adjustment is almost always used as the last step of every feature-based 3D reconstruction algorithm. It amounts to an optimization problem on the 3D structure and viewing parameters (i.e., camera pose and possibly intrinsic calibration and radial distortion), to obtain a reconstruction which is optimal under certain assumptions regarding the noise pertaining to the observed^[1] image features: If the image error is zero-mean Gaussian, then bundle adjustment is the Maximum Likelihood Estimator.^[2]{{rp|2}} Its name refers to the bundles of light rays originating from each 3D feature and converging on each camera's optical center, which are adjusted optimally with respect to both the structure and viewing parameters (similarity in meaning to categorical bundle seems a pure coincidence). Bundle adjustment was originally conceived in the field of photogrammetry during the 1950s and has increasingly been used by computer vision researchers during recent years.^[2]{{rp|2}}

General approach

Bundle adjustment boils down to minimizing the reprojection error between the image locations of

observed and predicted image points, which is expressed as the sum of squares of a large number of nonlinear, real-valued functions. Thus, the minimization is achieved using nonlinear least-squares algorithms. Of these, Levenberg–Marquardt has proven to be one of the most successful due to its ease of implementation and its use of an effective damping strategy that lends it the ability to converge quickly from a wide range of initial guesses. By iteratively linearizing the function to be minimized in the neighborhood of the current estimate, the Levenberg–Marquardt algorithm involves the solution of linear systems termed the normal equations. When solving the minimization problems arising in the framework of

bundle adjustment, the normal equations have a sparse block structure owing to the lack of interaction among parameters for different 3D points and cameras. This can be exploited to gain tremendous computational benefits by employing a sparse variant of the Levenberg–Marquardt algorithm which explicitly takes advantage of the normal equations zeros pattern, avoiding storing and operating on zero-elements.^[2]{{rp|3}}

Mathematical definition

Bundle adjustment amounts to jointly refining a set of initial camera and structure parameter estimates for finding the set of parameters that most accurately predict the locations of the observed points in the set of available images. More formally,^[3] assume that 3D points are seen in views and let 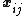be the projection of the th point on image . Let 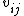denote the binary variables that equal 1 if point is visible in image and 0 otherwise. Assume also that each camera is parameterized by a vector 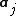and each 3D point by a vector 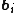. Bundle adjustment minimizes the total reprojection error with respect to all 3D point and camera parameters, specifically

where 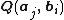is the predicted projection of point on image and 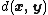denotes the Euclidean distance between the image points represented by vectors and . Clearly, bundle adjustment is by definition tolerant to missing image projections and minimizes a physically meaningful criterion.

Software

: Apero/MicMac, a free open source photogrammetric software. Cecill-B licence.
sba: A Generic Sparse Bundle Adjustment C/C++ Package Based on the Levenberg–Marquardt Algorithm (C, MATLAB). GPL.
cvsba: An OpenCV wrapper for sba library (C++). GPL.
[https://github.com/royshil/SfM-Toy-Library/tree/335d7d2a0c1e603ec994d0e025bdec8ebeb493bc/3rdparty/SSBA-3.0 ssba]: Simple Sparse Bundle Adjustment package based on the Levenberg–Marquardt Algorithm (C++). LGPL.
OpenCV: Computer Vision library in the Images stitching module. BSD license.
mcba: Multi-Core Bundle Adjustment (CPU/GPU). GPL3.
[https://github.com/dkogan/libdogleg libdogleg]: General-purpose sparse non-linear least squares solver, based on Powell's dogleg method. LGPL.
ceres-solver: A Nonlinear Least Squares Minimizer. BSD license.
g2o: General Graph Optimization (C++) - framework with solvers for sparse graph-based non-linear error functions. LGPL.
DGAP: The program DGAP implement the photogrammetric method of bundle adjustment invented by Helmut Schmid and Duane Brown. GPL.
[https://www.cs.cornell.edu/~snavely/bundler/ Bundler]: A structure-from-motion (SfM) system for unordered image collections (for instance, images from the Internet) by Noah Snavely. GPL.

References

1. ^{{cite conference |title=Bundle Adjustment — A Modern Synthesis |author=B. Triggs |author2=P. McLauchlan |author3=R. Hartley |author4=A. Fitzgibbon |booktitle=ICCV '99: Proceedings of the International Workshop on Vision Algorithms |pages=298–372 |doi=10.1007/3-540-44480-7_21 | isbn=3-540-67973-1 |publisher=Springer-Verlag |year=1999}}
2. ^¹²{{cite journal |title=SBA: A Software Package for Generic Sparse Bundle Adjustment |author=M.I.A. Lourakis and A.A. Argyros |journal=ACM Transactions on Mathematical Software |pages=1–30 |volume=36 |issue=1 |doi=10.1145/1486525.1486527 |year=2009}}
3. ^{{cite book |author=R.I. Hartley and A. Zisserman |title=Multiple View Geometry in computer vision |publisher=Cambridge University Press |edition=2nd |year=2004 |isbn=978-0-521-54051-3}}

Uses

General approach

Mathematical definition

Software

See also

References

Further reading