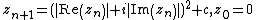“Burning Ship fractal”的意思、由来-开放百科全书

词条

Burning Ship fractal

释义

Implementation
References
External links

The Burning Ship fractal, first described and created by Michael Michelitsch and Otto E. Rössler in 1992, is generated by iterating the function:

in the complex plane 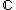which will either escape or remain bounded. The difference between this calculation and that for the Mandelbrot set is that the real and imaginary components are set to their respective absolute values before squaring at each iteration. The mapping is non-analytic because its real and imaginary parts do not obey the Cauchy–Riemann equations.^[1]

{{Gallery
|title=Burning Ship fractal renderings
|align=center
|height=125
|lines=5
|File:Burning Ship 3e-9.jpg|High-quality deep-zoom image of a small ship in the armada in the left Western antenna of the main ship structure
|File:Burning Ship Deep Zoom 2e-50.jpg|Burning Ship deep zoom to 2.3·10⁻⁵⁰
|File:Burning Ship Fractal.png|The Burning Ship fractal
|File:Burning Ship Fractal Zoom.png|A zoom-in to the lower left of the Burning Ship fractal, showing a "burning ship" and self-similarity to the complete fractal
|File:Burning Ship Fractal Zoom 2.png|A zoom-in to line on the left of the fractal, showing nested repetition (a different colour scheme is used here)
|File:Burning Ship 144x.jpg|High-quality image of the Burning Ship fractal
|File:Jentererforetrukket.jpg|The Burning Ship fractal featured in the 1K intro "JenterErForetrukket" by Youth Uprising; a demoscene production
|File:A Corresponding Julia Set of Burning Ship Fractal 2.PNG|A corresponding Julia set of Burning Ship fractal
|File:A Corresponding Julia Set of Burning Ship Fractal.PNG|A corresponding Julia set of Burning Ship fractal
}}

Implementation

The below pseudocode implementation hardcodes the complex operations for Z. Consider implementing complex number operations to allow for more dynamic and reusable code. Note that the typical images of the Burning Ship fractal display the ship upright: the actual fractal, and that produced by the below pseudocode, is inverted along the x-axis.

For each pixel (x, y) on the screen, do:

{

    x = scaled x coordinate of pixel (scaled to lie in the Mandelbrot X scale (-2.5, 1))    y = scaled y coordinate of pixel (scaled to lie in the Mandelbrot Y scale (-1, 1))               zx = x; // zx represents the real part of z    zy = y; // zy represents the imaginary part of z

      iteration = 0    max_iteration = 1000      while (zx*zx + zy*zy < 4  AND  iteration < max_iteration)     {        xtemp = zx*zx - zy*zy + x        zy = abs(2*zx*zy) + y //abs returns the absolute value        zx = abs(xtemp)

        iteration = iteration + 1    }

    if (iteration == max_iteration) //Belongs to the set        return insideColor;

}

References

1. ^Michael Michelitsch and Otto E. Rössler (1992). "The "Burning Ship" and Its Quasi-Julia Sets". In: Computers & Graphics Vol. 16, No. 4, pp. 435–438, 1992. Reprinted in Clifford A. Pickover Ed. (1998). Chaos and Fractals: A Computer Graphical Journey — A 10 Year Compilation of Advanced Research. Amsterdam, Netherlands: Elsevier. {{ISBN|0-444-50002-2}}

External links

[https://web.archive.org/web/20001003150909/http://www.theory.org/fracdyn/burningship/ About properties and symmetries of the Burning Ship fractal], featured by Theory.org
Burning Ship Fractal, Description and C source code.
Burning Ship with its Mset of higher powers and Julia Sets
Burningship, Video,
[https://web.archive.org/web/20110821220641/http://michelitsch-fractals.webs.com/Michelitsch_Fractals.htm Fractal webpage] includes the first representations and the original paper cited above on the Burning Ship fractal.
3D representations of the Burning Ship fractal
[https://7affer.github.io/fractalTS/ FractalTS] Mandelbrot, Burning ship and corresponding Julia set generator.

1 : Fractals

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。