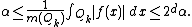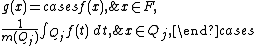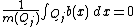“Calderón–Zygmund lemma”的意思、由来-开放百科全书

词条

Calderón–Zygmund lemma

释义

Covering lemma
Calderón–Zygmund decomposition
See also
References

In mathematics, the Calderón–Zygmund lemma is a fundamental result in Fourier analysis, harmonic analysis, and singular integrals. It is named for the mathematicians Alberto Calderón and Antoni Zygmund.

Given an integrable function {{math| f : R^d → C}}, where {{math|R^d}} denotes Euclidean space and {{math|C}} denotes the complex numbers, the lemma gives a precise way of partitioning {{math|R^d}} into two sets: one where {{math| f }} is essentially small; the other a countable collection of cubes where {{math| f }} is essentially large, but where some control of the function is retained.

This leads to the associated Calderón–Zygmund decomposition of {{math| f }}, wherein {{math| f }} is written as the sum of "good" and "bad" functions, using the above sets.

Covering lemma

Let {{math| f : R^d → C}} be integrable and {{mvar|α}} be a positive constant. Then there exists an open set {{math|Ω}} such that:
(1) {{math|Ω}} is a disjoint union of open cubes, {{math|Ω {{=}} ∪_k Q_k}}, such that for each {{math|Q_k}},
(2) {{math|{{!}} f (x){{!}} ≤ α}} almost everywhere in the complement {{mvar|F}} of {{math|Ω}}.

Calderón–Zygmund decomposition

Given {{math| f }} as above, we may write {{math| f }} as the sum of a "good" function {{mvar|g}} and a "bad" function {{mvar|b}}, {{math| f {{=}} g + b}}. To do this, we define
and let {{math|b {{=}} f − g}}. Consequently we have that
for each cube {{math|Q_j}}.

The function {{mvar|b}} is thus supported on a collection of cubes where {{math| f }} is allowed to be "large", but has the beneficial property that its average value is zero on each of these cubes. Meanwhile, {{math|{{!}}g(x){{!}} ≤ α}} for almost every {{mvar|x}} in {{mvar|F}}, and on each cube in {{math|Ω}}, {{mvar|g}} is equal to the average value of {{math| f }} over that cube, which by the covering chosen is not more than {{math|2^dα}}.

References

{{citation|author=Calderon A. P., Zygmund, A.|title=On the existence of certain singular integrals|journal=Acta Math|volume=88|year=1952|pages=85–139}}
{{citation|first=Lars|last= Hörmander|authorlink=Lars Hörmander|title=The analysis of linear partial differential operators, I. Distribution theory and Fourier analysis|edition=2nd|publisher=Springer-Verlag|year=1990|isbn= 3-540-52343-X}}
{{cite book|last = Stein |first = Elias|authorlink = Elias Stein|chapter = Chapters I–II|title = Singular Integrals and Differentiability Properties of Functions | publisher = Princeton University Press | year = 1970}}

2 : Theorems in Fourier analysis|Lemmas

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Covering lemma

Calderón–Zygmund decomposition

See also

References