“Carathéodory–Jacobi–Lie theorem”的意思、由来-开放百科全书

词条

Carathéodory–Jacobi–Lie theorem

释义

Statement
Applications
References

The Carathéodory–Jacobi–Lie theorem is a theorem in symplectic geometry which generalizes Darboux's theorem.

Statement

Let M be a 2n-dimensional symplectic manifold with symplectic form ω. For p ∈ M and r ≤ n, let f₁, f₂, ..., f_r be smooth functions defined on an open neighborhood V of p whose differentials are linearly independent at each point, or equivalently

where {f_i, f_j} = 0. (In other words, they are pairwise in involution.) Here {–,–} is the Poisson bracket. Then there are functions f_r+1, ..., f_n, g₁, g₂, ..., g_n defined on an open neighborhood U ⊂ V of p such that (f_i, g_i) is a symplectic chart of M, i.e., ω is expressed on U as

Applications

As a direct application we have the following. Given a Hamiltonian system as where M is a symplectic manifold with symplectic form 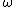and H is the Hamiltonian function, around every point where there is a symplectic chart such that one of its coordinates is H.

References

Lee, John M., Introduction to Smooth Manifolds, Springer-Verlag, New York (2003) {{ISBN|0-387-95495-3}}. Graduate-level textbook on smooth manifolds.

2 : Symplectic geometry|Theorems in differential geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。