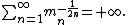“Carleman's condition”的意思、由来-开放百科全书

词条

Carleman's condition

释义

Hamburger moment problem
Stieltjes moment problem
Notes
References

In mathematics, particularly, in analysis, Carleman's condition gives a sufficient condition for the determinacy of the moment problem. That is, if a measure μ satisfies Carleman's condition, there is no other measure ν having the same moments as μ. The condition was discovered by Torsten Carleman in 1922.^[1]

Hamburger moment problem

For the Hamburger moment problem (the moment problem on the whole real line), the theorem states the following:

Let μ be a measure on R such that all the moments

are finite. If

then the moment problem for m_n is determinate; that is, μ is the only measure on R with (m_n) as its sequence of moments.

Stieltjes moment problem

For the Stieltjes moment problem, the sufficient condition for determinacy is

Notes

1. ^{{harvtxt|Akhiezer|1965}}

References

{{Cite book |first=N. I. |last=Akhiezer |title=The Classical Moment Problem and Some Related Questions in Analysis |publisher=Oliver & Boyd |year=1965|ref=harv }}

3 : Mathematical analysis|Probability theory|Theorems in approximation theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。