- Binary representation
- Primes and modular restrictions
- Generalizations
- References
- External links
A Carol number is an integer of the form 
. An equivalent formula is 
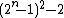. The first few Carol numbers are: −1, 7, 47, 223, 959, 3967, 16127, 65023, 261119, 1046527 {{OEIS|id=A093112}}.
Carol numbers were first studied by Cletus Emmanuel, who named them after a friend, Carol G. Kirnon.[1][2]
Binary representation
For n > 2, the binary representation of the n-th Carol number is n − 2 consecutive ones, a single zero in the middle, and n + 1 more consecutive ones, or to put it algebraically,
So, for example, 47 is 101111 in binary, 223 is 11011111, etc. The difference between the 2n-th Mersenne number and the n-th Carol number is 
. This gives yet another equivalent expression for Carol numbers, 
. The difference between the n-th Kynea number and the n-th Carol number is the (n + 2)th power of two.
Primes and modular restrictions
Starting with 7, every third Carol number is a multiple of 7. Thus, for a Carol number to also be a prime number, its index n cannot be of the form 3x + 2 for x > 0. The first few Carol numbers that are also prime are 7, 47, 223, 3967, 16127 (these are listed in Sloane's {{OEIS2C|id=A091516}}).
The 7th Carol number and 5th Carol prime, 16127, is also a prime when its digits are reversed, so it is the smallest Carol emirp.[3] The 12th Carol number and 7th Carol prime, 16769023, is also a Carol emirp.[4]
{{As of|2018|2}}, the largest known prime Carol number has index n = 695631, which has 418812 digits.[5][6] It was found by Mark Rodenkirch in July 2016 using the programs CKSieve and PrimeFormGW. It is the 44th Carol prime.Generalizations
A generalized Carol number base b is defined to be a number of the form (bn−1)2 − 2 with n ≥ 1, a generalized Carol number base b can be prime only if b is even, since if b is odd, then all generalized Carol numbers base b are even and thus not prime. A generalized Carol number to base bn is also a generalized Carol number to base b.
Least n ≥ 1 such that ((2b)n−1)2 − 2 is prime are
2, 1, 1, 1, 1, 3, 1, 1, 2, 1, 1, 2, 159, 1, 1, 2, 1, 1, 1, 4, 3, 1, 12, 1, 1, 2, 9, 1, 88, 2, 1, 1, 12, 4, 1, 1, 183, 1, 1, 320, 24, 4, 3, 2, 1, 3, 1, 5, 2, 4, 2, 1, 2, 1, 705, 2, 3, 29, 1, 1, 1, 4836, 20, 1, 135, 1, 4, 1, 6, 1, 15, 3912, 1, 2, 8, 3, 24, 1, 14, 4, 1, 2, 321, 11, 1, 174, 1, 6, 1, 42, 310, 1, 2, 27, 2, 1, 29, 3, 103, 20, ...
| b | numbers n ≥ 1 such that (bn−1)2 − 2 is prime (these n are checked up to 30000) | OEIS sequence |
| 2 | 2, 3, 4, 6, 7, 10, 12, 15, 18, 19, 21, 25, 27, 55, 129, 132, 159, 171, 175, 315, 324, 358, 393, 435, 786, 1459, 1707, 2923, 6462, 14289, 39012, 51637, 100224, 108127, 110953, 175749, 185580, 226749, 248949, 253987, 520363, 653490, 688042, 695631, ... | id=A091515}} |
| 4 | 1, 2, 3, 5, 6, 9, 66, 162, 179, 393, 3231, 19506, 50112, 92790, 326745, 344021, ... | |
| 6 | 1, 2, 6, 7, 20, 47, 255, 274, 279, 308, 1162, 2128, 3791, 9028, 9629, 10029, 13202, 38660, 46631, 48257, 117991, ... | id=A100901}} |
| 8 | 1, 2, 4, 5, 6, 7, 9, 43, 44, 53, 57, 105, 108, 131, 145, 262, 569, 2154, 4763, 13004, 33408, 58583, 61860, 75583, 82983, 217830, 231877, ... | |
| 10 | 1, 8, 21, 123, 4299, 6128, 11760, 18884, 40293, ... | id=A100903}} |
| 12 | 3, 29, 51, 7824, 15456, 22614, 28312, 47014, 68835, ... | |
| 14 | 1, 6, 13, 45, 74, 240, 553, 12348, 13659, 50603, ... | id=A100905}} |
| 16 | 1, 3, 33, 81, 9753, 25056, 46395, ... | |
| 18 | 2, 8, 30, 98, 110, 185, 912, 2514, 4074, 10208, 15123, 19395, ... | |
| 20 | 1, 2, 53, 183, 1281, 1300, 8041, 29936, 72820, ... | |
| 22 | 1, 8, 35, 88, 503, 8643, 8743, 14475, ... | id=A100907}} |
| 24 | 2, 27, 92, 4950, 20047, ... | |
| 26 | 159, 879, 4744, 5602, 74387, ... | |
| 28 | 1, 22, 127, 165, 2520, 6492, 6577, 22960, 25528, ... | |
| 30 | 1, 6, 19, 30, 166, 495, 769, 826, 1648, 3993, ... | |
| 32 | 2, 3, 5, 11, 35, 63, 87, 37116, 130698, ... | |
| 34 | 1, 4, 258, ... | |
| 36 | 1, 3, 10, 137, 154, 581, 1064, 4514, 6601, 19330, ... | |
| 38 | 1, 2, 13, 560, 28933, ... | |
| 40 | 4, 15, 39, 138, 2153, 4084, 5639, ... | |
| 42 | 3, 6, 14, 15, 29, 78, 195, 255, 272, 713, 2526, 4852, 10573, ... | |
| 44 | 1, 7, 30, 90, 1288, 1947, 12909, 25786, ... | |
| 46 | 12, 269, 1304, 5172, ... | |
| 48 | 1, 2, 4, 6, 12, 13, 3882, 6123, 15067, 15085, ... | |
| 50 | 1, 3, 4, 9, 31, 66, 115, 430, 1233, 2546, 2674, 6360, 53351, 69033, 69157, ... |
References
2. ^[https://groups.yahoo.com/neo/groups/primenumbers/conversations/messages/14584 Message to Yahoo primenumbers group] from Cletus Emmanuel
3. ^Prime Curios 16127 at Prime Pages
4. ^Prime Curios 16769023 at Prime Pages
5. ^Entry for 695631st Carol number at Prime Pages
6. ^Carol and Kynea Prime Search by Mark Rodenkirch
External links
- {{MathWorld|title=Near-Square Prime|urlname=Near-SquarePrime}}
- Prime Database entry for Carol(695631)
- Carol and Kynea Primes
- Carol and Kynea Prime Search
- Legislative Route 291 (California pre-1964)
- Legislative Route 292 (California pre-1964)
- Legislative Route 293 (California pre-1964)
- Legislative Route 294 (California pre-1964)
- Legislative Route 295 (California pre-1964)
- Legislative Route 296 (California pre-1964)
- Legislative Route 29 (California pre-1964)
- Legislative Route 2 (California pre-1964)
- Legislative Route 30 (California 1910s)
- Legislative Route 30 (California pre-1964)
- Legislative Route 31 (California pre-1964)
- Legislative Route 32 (California pre-1964)
- Legislative Route 33 (California pre-1964)
- Legislative Route 34 (California pre-1964)
- Legislative Route 35009 Parallel (Pennsylvania)
- Legislative Route 35 (California pre-1964)
- Legislative Route 37 (California pre-1964)
- Legislative Route 382 (Minnesota)
- Legislative Route 383 (Minnesota)
- Legislative Route 384 (Minnesota)
- Legislative Route 385 (Minnesota)
- Legislative Route 38 (California pre-1964)
- Legislative Route 390 (Minnesota)
- Legislative Route 391 (Minnesota)
- Legislative Route 392 (Minnesota)