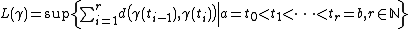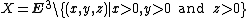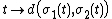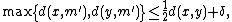- Definitions
- Examples
- Hadamard spaces
- Properties of
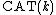 spaces
spaces - See also
- References
In mathematics, a 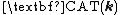 space, where
space, where  is a real number, is a specific type of metric space. Intuitively, triangles in a
is a real number, is a specific type of metric space. Intuitively, triangles in a 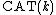 space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature
space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature  . In a
. In a 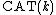 space, the curvature is bounded from above by
space, the curvature is bounded from above by  . A notable special case is
. A notable special case is  ; complete
; complete 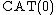 spaces are known as Hadamard spaces after the French mathematician Jacques Hadamard.
spaces are known as Hadamard spaces after the French mathematician Jacques Hadamard.
Originally, Aleksandrov called these spaces “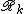 domain”.
domain”.
The terminology 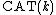 was coined by Mikhail Gromov in 1987 and is an acronym for Élie Cartan, Aleksandr Danilovich Aleksandrov and Victor Andreevich Toponogov (although Toponogov never explored curvature bounded above in publications).
was coined by Mikhail Gromov in 1987 and is an acronym for Élie Cartan, Aleksandr Danilovich Aleksandrov and Victor Andreevich Toponogov (although Toponogov never explored curvature bounded above in publications).
Definitions
For a real number  , let
, let  denote the unique complete simply connected surface (real 2-dimensional Riemannian manifold) with constant curvature
denote the unique complete simply connected surface (real 2-dimensional Riemannian manifold) with constant curvature  . Denote by
. Denote by 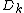 the diameter of
the diameter of  , which is
, which is  if
if 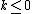 and
and 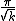 for
for 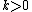 .
.
Let  be a geodesic metric space, i.e. a metric space for which every two points
be a geodesic metric space, i.e. a metric space for which every two points 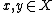 can be joined by a geodesic segment, an arc length parametrized continuous curve
can be joined by a geodesic segment, an arc length parametrized continuous curve 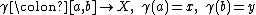 , whose length
, whose length
is precisely  . Let
. Let  be a triangle in
be a triangle in 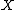 with geodesic segments as its sides.
with geodesic segments as its sides.  is said to satisfy the
is said to satisfy the 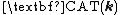 inequality if there is a comparison triangle
inequality if there is a comparison triangle 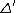 in the model space
in the model space  , with sides of the same length as the sides of
, with sides of the same length as the sides of  , such that distances between points on
, such that distances between points on  are less than or equal to the distances between corresponding points on
are less than or equal to the distances between corresponding points on 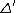 .
.
The geodesic metric space  is said to be a
is said to be a 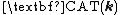 space if every geodesic triangle
space if every geodesic triangle  in
in 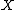 with perimeter less than
with perimeter less than 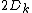 satisfies the
satisfies the 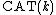 inequality. A (not-necessarily-geodesic) metric space
inequality. A (not-necessarily-geodesic) metric space 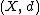 is said to be a space with curvature
is said to be a space with curvature 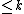 if every point of
if every point of 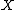 has a geodesically convex
has a geodesically convex 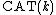 neighbourhood. A space with curvature
neighbourhood. A space with curvature 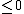 may be said to have non-positive curvature.
may be said to have non-positive curvature.
Examples
- Any
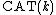 space
space  is also a
is also a 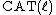 space for all
space for all 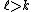 . In fact, the converse holds: if
. In fact, the converse holds: if  is a
is a 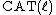 space for all
space for all 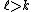 , then it is a
, then it is a 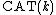 space.
space. - The
 -dimensional Euclidean space
-dimensional Euclidean space 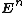 with its usual metric is a
with its usual metric is a 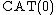 space. More generally, any real inner product space (not necessarily complete) is a
space. More generally, any real inner product space (not necessarily complete) is a 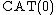 space; conversely, if a real normed vector space is a
space; conversely, if a real normed vector space is a 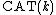 space for some real
space for some real  , then it is an inner product space.
, then it is an inner product space. - The
 -dimensional hyperbolic space
-dimensional hyperbolic space 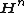 with its usual metric is a
with its usual metric is a 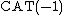 space, and hence a
space, and hence a 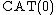 space as well.
space as well. - The
 -dimensional unit sphere
-dimensional unit sphere  is a
is a 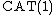 space.
space. - More generally, the standard space
 is a
is a 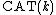 space. So, for example, regardless of dimension, the sphere of radius
space. So, for example, regardless of dimension, the sphere of radius  (and constant curvature
(and constant curvature 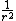 ) is a
) is a 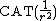 space. Note that the diameter of the sphere is
space. Note that the diameter of the sphere is 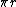 (as measured on the surface of the sphere) not
(as measured on the surface of the sphere) not 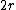 (as measured by going through the centre of the sphere).
(as measured by going through the centre of the sphere). - The punctured plane
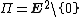 is not a
is not a 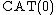 space since it is not geodesically convex (for example, the points
space since it is not geodesically convex (for example, the points  and
and 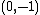 cannot be joined by a geodesic in
cannot be joined by a geodesic in  with arc length 2), but every point of
with arc length 2), but every point of  does have a
does have a 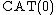 geodesically convex neighbourhood, so
geodesically convex neighbourhood, so  is a space of curvature
is a space of curvature 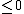 .
. - The closed subspace
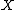 of
of 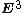 given by
given by
equipped with the induced length metric is not aspace for any
.
- Any product of
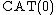 spaces is
spaces is 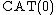 . (This does not hold for negative arguments.)
. (This does not hold for negative arguments.)
Hadamard spaces
{{main|Hadamard space}}As a special case, a complete CAT(0) space is also known as a Hadamard space; this is by analogy with the situation for Hadamard manifolds. A Hadamard space is contractible (it has the homotopy type of a single point) and, between any two points of a Hadamard space, there is a unique geodesic segment connecting them (in fact, both properties also hold for general, possibly incomplete, CAT(0) spaces). Most importantly, distance functions in Hadamard spaces are convex: if 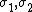 are two geodesics in X defined on the same interval of time I, then the function
are two geodesics in X defined on the same interval of time I, then the function 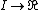 given by
given by
is convex in t.
Properties of 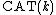 spaces
spaces
Let  be a
be a 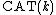 space. Then the following properties hold:
space. Then the following properties hold:
- Given any two points
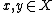 (with
(with 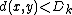 if
if 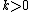 ), there is a unique geodesic segment that joins
), there is a unique geodesic segment that joins  to
to  ; moreover, this segment varies continuously as a function of its endpoints.
; moreover, this segment varies continuously as a function of its endpoints. - Every local geodesic in
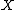 with length at most
with length at most 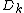 is a geodesic.
is a geodesic. - The
 -balls in
-balls in 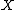 of radius less than
of radius less than 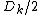 are (geodesically) convex.
are (geodesically) convex. - The
 -balls in
-balls in 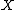 of radius less than
of radius less than 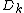 are contractible.
are contractible. - Approximate midpoints are close to midpoints in the following sense: for every
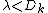 and every
and every 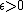 there exists a
there exists a 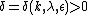 such that, if
such that, if  is the midpoint of a geodesic segment from
is the midpoint of a geodesic segment from  to
to  with
with 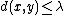 and
and
then.
- It follows from these properties that, for
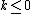 the universal cover of every
the universal cover of every 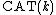 space is contractible; in particular, the higher homotopy groups of such a space are trivial. As the example of the
space is contractible; in particular, the higher homotopy groups of such a space are trivial. As the example of the  -sphere
-sphere  shows, there is, in general, no hope for a
shows, there is, in general, no hope for a 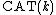 space to be contractible if
space to be contractible if 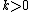 .
. - An
 -dimensional
-dimensional 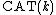 space equipped with the
space equipped with the  -dimensional Hausdorff measure satisfies the
-dimensional Hausdorff measure satisfies the  condition in the sense of John Lott, Cédric Villani, and Karl-Theodor Sturm.{{Citation needed|date=December 2013}}
condition in the sense of John Lott, Cédric Villani, and Karl-Theodor Sturm.{{Citation needed|date=December 2013}}
See also
- Cartan–Hadamard theorem
References
- {{cite web
| last = Alexander
| first = S.
|author2=Kapovitch V.|author3=Petrunin A.
| title = Alexandrov Geometry, Chapter 7
| url = http://www.math.uiuc.edu/~sba/the-defs-CBA.pdf
| format = PDF
| accessdate = 2011-04-07
}}
- {{cite arXiv |last1= Alexander|first1= Stephanie|last2=Kapovitch|first2=Vitali|last3=Petrunin|first3=Anton|eprint= 1701.03483|title= Invitation to Alexandrov geometry: CAT[0] spaces|class= math.DG}}
- {{cite book
| last = Ballmann
| first = Werner
| title = Lectures on spaces of nonpositive curvature
| series = DMV Seminar 25
| publisher = Birkhäuser Verlag
| location = Basel
| year = 1995
| pages = viii+112
| isbn = 3-7643-5242-6
| mr = 1377265
}}
- {{cite book
| last = Bridson
| first = Martin R.
|author2=Haefliger, André
| title = Metric spaces of non-positive curvature
| series = Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences] 319
| publisher = Springer-Verlag
| location = Berlin
| year = 1999
| pages = xxii+643
| isbn = 3-540-64324-9
| mr = 1744486
}}
- {{cite book
| last = Gromov
| first = Mikhail
| authorlink = Mikhail Gromov (mathematician)
| chapter = Hyperbolic groups
| title = Essays in group theory
| series = Math. Sci. Res. Inst. Publ. 8
| pages = 75–263
| publisher = Springer
| location = New York
| year = 1987
| mr = 919829
}}
- {{cite book
| last = Hindawi
| first = Mohamad A.
| title = Asymptotic invariants of Hadamard manifolds
| publisher = PhD thesis
| location = University of Pennsylvania
| url = http://www.math.upenn.edu/grad/dissertations/HindawiThesis.pdf
| year = 2005
}}
- Thulopatal
- Thulo Pokhara
- Thulo Sirubari
- Thulsa Doom (album)
- Thulsa Doom (comics)
- Thulsa Doom (Robert E. Howard)
- Thul Taluka
- Thulth
- Thulu
- Thuluva Vellala Mudaliar
- Thuluva Vellalar
- Thumaita
- Thumakodada
- Thumamah Airport
- Thuman
- Thuma Peak
- Thumatha
- Thumatha senex
- Thumathoides
- Thu Maung
- Thumb-2
- Thumbara
- Thumb Area Bottomland Preserve
- Thumb (backhoe)
- Thumb Bible