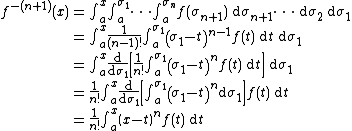“Cauchy formula for repeated integration”的意思、由来-开放百科全书

词条

Cauchy formula for repeated integration

释义

Scalar case
Applications
References
External links

The Cauchy formula for repeated integration, named after Augustin Louis Cauchy, allows one to compress n antidifferentiations of a function into a single integral (cf. Cauchy's formula).

Scalar case

Let ƒ be a continuous function on the real line. Then the nth repeated integral of ƒ based at a,

,

is given by single integration

.

A proof is given by induction. Since ƒ is continuous, the base case follows from the Fundamental theorem of calculus:

;

where

.

Now, suppose this is true for n, and let us prove it for n+1. Firstly, using the Leibniz integral rule, note that

.

Then, applying the induction hypothesis,

This completes the proof.

Applications

In fractional calculus, this formula can be used to construct a notion of differintegral, allowing one to differentiate or integrate a fractional number of times. Integrating a fractional number of times with this formula is straightforward; one can use fractional n by interpreting (n-1)! as Γ(n) (see Gamma function). Differentiating a fractional number of times can be accomplished by fractional integration, then differentiating the result.

References

Gerald B. Folland, Advanced Calculus, p. 193, Prentice Hall (2002). {{ISBN|0-13-065265-2}}

External links

{{cite web|author=Alan Beardon|url=http://nrich.maths.org/public/viewer.php?obj_id=1369|title=Fractional calculus II|publisher=University of Cambridge|year=2000}}

2 : Integral calculus|Theorems in analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。