“Central subgroup”的意思、由来-开放百科全书

词条

Central subgroup

释义

References

In mathematics, in the field of group theory, a subgroup of a group is termed central if it lies inside the center of the group.

Given a group , the center of , denoted as 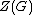, is defined as the set of those elements of the group which commute with every element of the group. The center is a characteristic subgroup and is also an abelian group (because, in particular, all elements of the center must commute with each other). A subgroup of is termed central if .

Central subgroups have the following properties:

They are abelian groups.
They are normal subgroups. They are central factors, and are hence transitively normal subgroups.

References

{{springer|id=C/c021250|title=Centre of a group}}.

1 : Subgroup properties

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。