万能置换法解三角方程wanneng zhihuanfa jie sanjiaofangcheng
解三角方程的一种方法.其特点是对方程中的所有三角函数施用万能代换,使三角方程转化为代数方程,以便用代数方法来求解.
| 例 解方程 |
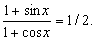
| 解 设 |
| tgx/2=t, |
| 则 |
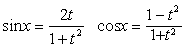
| 代入原方程并化简,得关 |
若 tg(x/2)=t=0,则x=2kπ
若 tg(x/2)=t=-2,则x=2(kπ-arctg2)
故x=2kπ,x=2(kπ-arctg2)(k∈Z)
经检验x=(2k+1)π不是原方程的根,所以原方程没有遗根.
应用万能置换法,不但可能使原方程遗根,有时还会引进高次方程,所以若有别的方法,就不用万能置换法.