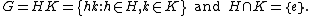1. Properties

2. Relation to other products

3. Existence

4. See also

5. References

In mathematics, especially in the area of algebra known as group theory, a complement of a subgroup H in a group G is a subgroup K of G such that

Equivalently, every element of G has a unique expression as a product hk where h ∈ H and k ∈ K. This relation is symmetrical: if K is a complement of H, then H is a complement of K. Neither H nor K need be a normal subgroup of G.

Properties

• Complements need not exist, and if they do they need not be unique. That is, H could have two distinct complements K₁ and K₂ in G.
• If there are several complements of a normal subgroup, then they are necessarily isomorphic to each other and to the quotient group.
• If K is a complement of H in G then K forms both a left and right transversal of H That is, the elements of K form a complete set of representatives of both the left and right cosets of H.
• The Schur–Zassenhaus theorem guarantees the existence of complements of normal Hall subgroups of finite groups.

Relation to other products

Complements generalize both the direct product (where the subgroups H and K are normal in G), and the semidirect product (where one of H or K is normal in G). The product corresponding to a general complement is called the internal Zappa–Szép product. When H and K are nontrivial, complement subgroups factor a group into smaller pieces.

Existence

As previously mentioned, complements need not exist.

A p-complement is a complement to a Sylow p-subgroup. Theorems of Frobenius and Thompson describe when a group has a normal p-complement. Philip Hall characterized finite soluble groups amongst finite groups as those with p-complements for every prime p; these p-complements are used to form what is called a Sylow system.

A Frobenius complement is a special type of complement in a Frobenius group.

A complemented group is one where every subgroup has a complement.

See also

• Product of group subsets

References

• {{cite book | author=David S. Dummit & Richard M. Foote | title=Abstract Algebra | publisher=Wiley | year=2003 | isbn=978-0-471-43334-7}}
• {{cite book | author=I. Martin Isaacs | title=Finite Group Theory | publisher=American Mathematical Society | year=2008 | isbn=978-0-8218-4344-4 }}

• Zabi Rog
• Zabita Khan
• Zabitek
• Zabiullah Mujahid
• Zabiče
• Zabja vas
• Zabjek v Podbocju
• Zab Judah vs. Lucas Matthysse
• Zabka
• Zabka, Opole Voivodeship
• Zabki (disambiguation)
• Zabki, Lodz Voivodeship
• Zabki, West Pomeranian Voivodeship
• Zabkow
• Zabkowice Slaskie Commune
• Zabkowicki
• Zablace (Cacak)
• Zablace (Sabac)
• Zablati (Bohumin)
• Zablati (Jindrichuv Hradec District)
• Zablati (Prachatice District)
• Zablati (Zdar nad Sazavou District)
• Zablatje
• Zablaće (Čačak)
• Zablaće (Šabac)