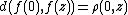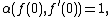“Complex geodesic”的意思、由来-开放百科全书

词条

Complex geodesic

释义

Definition
Properties and examples of complex geodesics
References

In mathematics, a complex geodesic is a generalization of the notion of geodesic to complex spaces.

Definition

Let (X, || ||) be a complex Banach space and let B be the open unit ball in X. Let Δ denote the open unit disc in the complex plane C, thought of as the Poincaré disc model for 2-dimensional real/1-dimensional complex hyperbolic geometry. Let the Poincaré metric ρ on Δ be given by

and denote the corresponding Carathéodory metric on B by d. Then a holomorphic function f : Δ → B is said to be a complex geodesic if

for all points w and z in Δ.

Properties and examples of complex geodesics

Given u ∈ X with ||u|| = 1, the map f : Δ → B given by f(z) = zu is a complex geodesic.
Geodesics can be reparametrized: if f is a complex geodesic and g ∈ Aut(Δ) is a bi-holomorphic automorphism of the disc Δ, then f o g is also a complex geodesic. In fact, any complex geodesic f₁ with the same image as f (i.e., f₁(Δ) = f(Δ)) arises as such a reparametrization of f.
If

for some z ≠ 0, then f is a complex geodesic.

where α denotes the Caratheodory length of a tangent vector, then f is a complex geodesic.

References

{{cite book

| author = Earle, Clifford J. and Harris, Lawrence A. and Hubbard, John H. and Mitra, Sudeb
| chapter = Schwarz's lemma and the Kobayashi and Carathéodory pseudometrics on complex Banach manifolds
| title = Kleinian groups and hyperbolic 3-manifolds (Warwick, 2001)
|editor1=Komori, Y. |editor2=Markovic, V. |editor3=Series, C. | series = London Math. Soc. Lecture Note Ser. 299
| pages = 363–384
|publisher = Cambridge Univ. Press
| location = Cambridge
| year = 2003
}}

2 : Hyperbolic geometry|Metric geometry

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。