1. Definition

2. Relation to Transducers

3. See also

4. Notes

5. References

6. External links

In formal language theory, a cone is a set of formal languages that has some desirable closure properties enjoyed by some well-known sets of languages, in particular by the families of regular languages, context-free languages and the recursively enumerable languages.^[1] The concept of a cone is a more abstract notion that subsumes all of these families. A similar notion is the faithful cone, having somewhat relaxed conditions. For example, the context-sensitive languages do not form a cone, but still have the required properties to form a faithful cone.

The terminology cone has a French origin. In the American oriented literature one usually speaks of a full trio. The trio corresponds to the faithful cone.

Definition

A cone is a family of languages such that contains at least one non-empty language, and for any 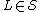over some alphabet ,

• if is a homomorphism from 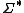to some 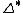, the language 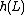is in ;
• if is a homomorphism from some 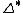to 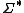, the language 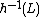is in ;
• if is any regular language over , the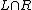n is in .

The family of all regular languages is contained in any cone.

If one restricts the definition to homomorphisms that do not introduce the empty word then one speaks of a faithful cone; the inverse homomorphisms are not restricted. Within the Chomsky hierarchy, the regular languages, the context-free languages, and the recursively enumerable languages are all cones, whereas the context-sensitive languages and the recursive languages are only faithful cones.

Relation to Transducers

A finite state transducer is a finite state automaton that has both input and output. It defines a transduction 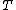, mapping a language over the input alphabet into another language 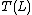over the output alphabet. Each of the cone operations (homomorphism, inverse homomorphism, intersection with a regular language) can be implemented using a finite state transducer. And, since finite state transducers are closed under composition, every sequence of cone operations can be performed by a finite state transducer.

Conversely, every finite state transduction 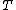can be decomposed into cone operations. In fact, there exists a normal form for this decomposition,^[2] which is commonly known as Nivat's Theorem:^[3]

Namely, each such 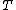can be effectively decomposed as

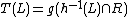, where 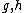are homomorphisms, and is a regular language depending only on .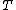

Altogether, this means that a family of languages is a cone if it is closed under finite state transductions. This is a very powerful set of operations. For instance one easily writes a (nondeterministic) finite state transducer with alphabet that removes every second in words of even length (and does not change words otherwise). Since the context-free languages form a cone, they are closed under this exotic operation.

See also

• Abstract family of languages

Notes

References

• {{cite conference

• {{Cite journal | last1 = Nivat | first1 = Maurice| authorlink1 = Maurice Nivat| doi = 10.5802/aif.287 | title = Transductions des langages de Chomsky | journal = Annales de l'Institut Fourier | volume = 18| number = 1| pages = 339–455| year = 1968 | pmid = | pmc = }}
• Seymour Ginsburg, Algebraic and automata theoretic properties of formal languages, North-Holland, 1975, {{ISBN|0-7204-2506-9}}.
• John E. Hopcroft and Jeffrey D. Ullman, Introduction to Automata Theory, Languages, and Computation, Addison-Wesley Publishing, Reading Massachusetts, 1979. {{ISBN|0-201-02988-X}}. Chapter 11: Closure properties of families of languages.
• {{cite book |last1=Mateescu | first1=Alexandru |last2=Salomaa|first2=Arto |editor1-first=Grzegorz| editor1-last=Rozenberg|editor2-first=Arto| editor2-last=Salomaa |title=Handbook of Formal Languages. Volume I: Word, language, grammar |publisher=Springer-Verlag |year=1997 |pages=175–252 |chapter=Chapter 4: Aspects of Classical Language Theory |isbn=3-540-61486-9}}

External links

• Encyclopedia of mathematics: Trio, Springer.

• Hiroi Ōji
• Hiroji Imamura
• Hiroji Kataoka
• Hiroji Kiyotake
• Hiroka
• Hirokage
• Hiro-Kala
• Hirokane Kenshi
• Hirokawa
• Hirokawa Beach Station
• Hirokawa Taichirou
• Hirokawa Taichirō
• Hiroka Yaginuma
• Hirokazu Goshi
• Hirokazu Hasegawa
• Hirokazu Ibata
• Hirokazu Kore-Eda
• Hirokazu Ninomiya
• Hirokazu Ota
• Hirokazu Otsubo
• Hirokazu Sasaki
• Hirokazu Ueyonabaru
• Hirokazu Usami
• Hiroki Aratani
• Hiroki Azuma (footballer)