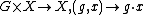“Continuous group action”的意思、由来-开放百科全书

词条

Continuous group action

释义

References
See also

In topology, a continuous group action on a topological space X is a group action of a topological group G that is continuous: i.e.,

is a continuous map. Together with the group action, X is called a G-space.

If 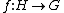is a continuous group homomorphism of topological groups and if X is a G-space, then H can act on X by restriction: 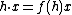, making X a H-space. Often f is either an inclusion or a quotient map. In particular, any topological space may be thought of as a G-space via (and G would act trivially.)

Two basic operations are that of taking the space of points fixed by a subgroup H and that of forming a quotient by H. We write 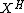for the set of all x in X such that 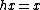. For example, if we write 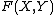for the set of continuous maps from a G-space X to another G-space Y, then, with the action ,

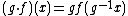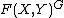consists of f such that 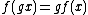; i.e., f is an equivariant map. We write 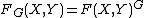. Note, for example, for a G-space X and a closed subgroup H, .

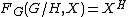References

John Greenlees, Peter May, Equivariant stable homotopy theory

References

See also