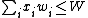“Continuous knapsack problem”的意思、由来-开放百科全书

In theoretical computer science, the continuous knapsack problem (also known as the fractional knapsack problem) is an algorithmic problem in combinatorial optimization in which the goal is to fill a container (the "knapsack") with fractional amounts of different materials chosen to maximize the value of the selected materials.^[1]^[2] It resembles the classic knapsack problem, in which the items to be placed in the container are indivisible; however, the continuous knapsack problem may be solved in polynomial time whereas the classic knapsack problem is NP-hard.^[1] It is a classic example of how a seemingly small change in the formulation of a problem can have a large impact on its computational complexity.

Problem definition

An instance of either the continuous or classic knapsack problems may be specified by the numerical capacity W of the knapsack, together with a collection of materials, each of which has two numbers associated with it: the weight w_i of material that is available to be selected and the value per unit weight v_i of that material. The goal is to choose an amount x_i ≤ w_i of each material, subject to the capacity constraint

In the classic knapsack problem, each of the amounts x_i must be either zero or w_i; the continuous knapsack problem differs by allowing x_i to range continuously from zero to w_i.^[1]

Some formulations of this problem rescale the variables x_i to be in the range from 0 to 1

Solution technique

The continuous knapsack problem may be solved by a greedy algorithm, first published in 1957 by George Dantzig,^[2]^[3] that considers the materials in sorted order by their values per unit weight. For each material, the amount x_i is chosen to be as large as possible:

Because of the need to sort the materials, this algorithm takes time O(n log n) on inputs with n materials.^[1]^[2] However, by adapting an algorithm for finding weighted medians, it is possible to solve the problem in time O(n).^[2]

References

1. ^¹²³{{citation|title=Algorithm Design: Foundations, Analysis, and Internet Examples|first1=Michael T.|last1=Goodrich|author1-link=Michael T. Goodrich|first2=Roberto|last2=Tamassia|author2-link=Roberto Tamassia|publisher=John Wiley & Sons|year=2002|contribution=5.1.1 The Fractional Knapsack Problem|pages=259–260}}.
2. ^¹²³{{citation|title=Combinatorial Optimization: Theory and Algorithms|volume=21|series=Algorithms and Combinatorics|first1=Bernhard|last1=Korte|author1-link=Bernhard Korte|first2=Jens|last2=Vygen|publisher=Springer|year=2012|isbn=9783642244889|contribution=17.1 Fractional Knapsack and Weighted Median|pages=459–461|url=https://books.google.com/books?id=8535vmYbLGYC&pg=PA459}}.
3. ^{{citation | last = Dantzig | first = George B. | authorlink = George Dantzig | doi = 10.1287/opre.5.2.266 | journal = Operations Research | mr = 0089098 | pages = 266–277 | title = Discrete-variable extremum problems | volume = 5 | year = 1957}}.