“Cook's distance”的意思、由来-开放百科全书

In statistics, Cook's distance or Cook's D is a commonly used estimate of the influence of a data point when performing a least-squares regression analysis.^[1] In a practical ordinary least squares analysis, Cook's distance can be used in several ways: to indicate influential data points that are particularly worth checking for validity; or to indicate regions of the design space where it would be good to be able to obtain more data points. It is named after the American statistician R. Dennis Cook, who introduced the concept in 1977.^[2]^[3]

Definition

Data points with large residuals (outliers) and/or high leverage may distort the outcome and accuracy of a regression. Cook's distance measures the effect of deleting a given observation. Points with a large Cook's distance are considered to merit closer examination in the analysis.

where

is the error term,

is the coefficient matrix,

is the number of covariates or predictors for each observation, and

is the design matrix including a constant. The least squares estimator then is

, and consequently the fitted (predicted) values for the mean of

are

where

is the projection matrix (or hat matrix). The

-th diagonal element of

, given by

,^[4] is known as the leverage of the

-th observation. Similarly, the

-th element of the residual vector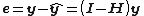

is denoted by

Cook's distance

of observation

is defined as the sum of all the changes in the regression model when observation

is removed from it^[5]

where

is the fitted response value obtained when excluding

, and

is the mean squared error of the regression model.^[6]

Detecting highly influential observations

There are different opinions regarding what cut-off values to use for spotting highly influential points. Since Cook's distance is in the metric of an F distribution with

and

(as defined for the design matrix

above) degrees of freedom, the median point (i.e.,

) can be used as a cut-off.^[7] Since this value is close to 1 for large

, a simple operational guideline of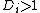

has been suggested.^[8]

Note that the Cook's distance measure does not always correctly identify influential observations.^[9]

Interpretation

Specifically

can be interpreted as the distance one's estimates move within the confidence ellipsoid that represents a region of plausible values for the parameters.{{Clarify|date=July 2010}} This is shown by an alternative but equivalent representation of Cook's distance in terms of changes to the estimates of the regression parameters between the cases, where the particular observation is either included or excluded from the regression analysis.

See also

References

1. ^{{cite book |last1= Mendenhall |first1= William |last2=Sincich |first2=Terry |title=A Second Course in Statistics: Regression Analysis |edition=5th |year=1996 |publisher=Prentice-Hall |location=Upper Saddle River, NJ |isbn=0-13-396821-9 |page=422 |quote=A measure of overall influence an outlying observation has on the estimated

coefficients was proposed by R. D. Cook (1979). Cook's distance, D_i, is calculated...}}
2. ^{{cite journal | last=Cook |first=R. Dennis | title=Detection of Influential Observations in Linear Regression | journal=Technometrics | volume=19 |issue=1 |pages= 15–18 |date=February 1977 | publisher=American Statistical Association | mr=0436478 | doi=10.2307/1268249 | jstor=1268249 }}
3. ^{{cite journal | last=Cook |first=R. Dennis | title=Influential Observations in Linear Regression | journal=Journal of the American Statistical Association | volume=74 |issue=365 |pages=169–174 |date=March 1979 | publisher=American Statistical Association | mr=0529533 | doi=10.2307/2286747 | jstor=2286747 }}
4. ^{{cite book |first=Fumio |last=Hayashi |title=Econometrics |location= |publisher=Princeton University Press |year=2000 |pages=21–23 |url=https://books.google.com/books?id=QyIW8WUIyzcC&pg=PA21 }}
5. ^¹{{cite web|url=http://se.mathworks.com/help/stats/cooks-distance.html|title=Cook's Distance}}
6. ^{{cite web |title=Statistics 512: Applied Linear Models |work=Purdue University |date= |url=https://www.stat.purdue.edu/~jennings/stat514/stat512notes/topic3.pdf#page=9 }}
7. ^{{cite book |last= Bollen |first= Kenneth A. |authorlink=Kenneth A. Bollen |last2=Jackman |first2=Robert W. |year=1990 |chapter= Regression Diagnostics: An Expository Treatment of Outliers and Influential Cases |editor-last= Fox |editor-first=John |editor2-last= Long |editor2-link=J. Scott Long|editor2-first=J. Scott |title= Modern Methods of Data Analysis |pages=257–91 [p. 266] |location= Newbury Park, CA |publisher= Sage |isbn=0-8039-3366-5 }}
8. ^{{cite book |last=Cook |first=R. Dennis |last2=Weisberg |first2=Sanford |authorlink2=Sanford Weisberg |year=1982 |title=Residuals and Influence in Regression |location=New York, NY |publisher=Chapman & Hall |isbn=0-412-24280-X |url=https://books.google.com/books?id=MVSqAAAAIAAJ }}
9. ^{{cite journal|first1=Myung Geun|last1=Kim|title=A cautionary note on the use of Cook's distance|url=http://www.csam.or.kr/journal/view.html?doi=10.5351/CSAM.2017.24.3.317|journal=Communications for Statistical Applications and Methods|date=31 May 2017|issn=2383-4757|pages=317–324|volume=24|issue=3|doi=10.5351/csam.2017.24.3.317}}

Definition

Detecting highly influential observations

Interpretation

See also

References

Further reading