- Definition
- Countable fan tightness
- Properties
- Examples
- See also
- External links
- References
In mathematics, a topological space X is called countably generated if the topology of X is determined by the countable sets in a similar way as the topology of a sequential space (or a Fréchet space) by the convergent sequences.
The countable generated spaces are precisely the spaces having countable tightness - therefore the name countably tight is used as well.
Definition
A topological space X is called countably generated if V is closed in X whenever for each countable subspace U of X the set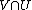 
is closed in U. Equivalently, X is countably generated if and only if the closure of any subset A of X equals the union of closures of all countable subsets of A.
Countable fan tightness
A topological space 
has countable fan tightness if for every point 
and every sequence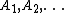 
of subsets of the space such that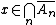 
, there are finite set 
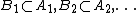such that 
.
A topological space has countable strong fan tightness if for every point and every sequence 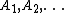of subsets of the space such that 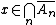, there are points 
such that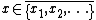 
. Every strong Fréchet–Urysohn space has strong countable fan tightness.
Properties
A quotient of countably generated space is again countably generated. Similarly, a topological sum of countably generated spaces is countably generated. Therefore the countably generated spaces form a coreflective subcategory of the category of topological spaces. They are the coreflective hull of all countable spaces.
Any subspace of a countably generated space is again countably generated.
Examples
Every sequential space (in particular, every metrizable space) is countably generated.
An example of a space which is countably generated but not sequential can be obtained, for instance, as a subspace of Arens–Fort space.
See also
- The concept of finitely generated space is related to this notion.
- Tightness is a cardinal function related to countably generated spaces and their generalizations.
External links
- A Glossary of Definitions from General Topology
- https://web.archive.org/web/20040917084107/http://thales.doa.fmph.uniba.sk/density/pages/slides/sleziak/paper.pdf
References
- {{cite book | last=Herrlich | first=Horst | title=Topologische Reflexionen und Coreflexionen | publisher = Springer| location=Berlin | year=1968 | id= | others=Lecture Notes in Math. 78}}
- Helen Wallace Stoepel
- Helen Wang
- Helen Warburton
- Helen Waterhouse
- Helen Watson Phelps
- Helen Watts (suffragette)
- Helen Wellings
- Helen West Heller
- Helen West (TV series)
- Helen Whitelaw Marshall Young
- Helen White Peterson
- Helen Wiggins
- Helen Wilkes
- Helen Wilkie
- Helen Williams (American fashion model)
- Helen Williams (curler)
- Helen Williams Jackson
- Helen Wilson (Australian judge)
- Helen Wilson Cargill
- Helen Wilson (mathematician)
- Helen Wily
- Helen Winkelmann
- Helen Winslow
- Helen Winslow Durkee
- Helen Wodehouse