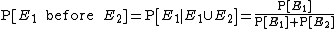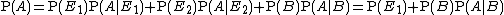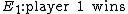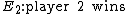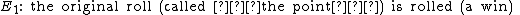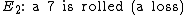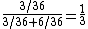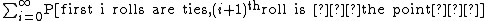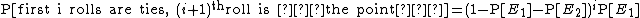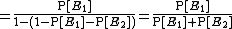“Craps principle”的意思、由来-开放百科全书

词条

Craps principle

释义

Proof
Application
Stopping
Craps example
References
Notes

In probability theory, the craps principle is a theorem about event probabilities under repeated iid trials. Let and 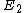denote two mutually exclusive events which might occur on a given trial. Then the probability that occurs before 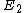equals the conditional probability that occurs given that or 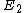occur on the next trial, which is

The events and 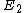need not be collectively exhaustive (if they are, the result is trivial).^[1]^[2]

Proof

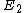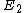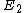Let be the event that occurs before . Let be the event that neither nor occurs on a given trial. Since , and are mutually exclusive and collectively exhaustive for the first trial, we have

and .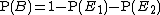

Since the trials are i.i.d., we have 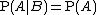. Using 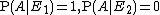and solving the displayed equation for 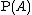gives the formula

.

Application

If the trials are repetitions of a game between two players, and the events are

then the craps principle gives the respective conditional probabilities of each player winning a certain repetition, given that someone wins (i.e., given that a draw does not occur). In fact, the result is only affected by the relative marginal probabilities of winning 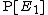and 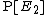; in particular, the probability of a draw is irrelevant.

Stopping

If the game is played repeatedly until someone wins, then the conditional probability above is the probability that the player wins the game. This is illustrated below for the original game of craps, using an alternative proof.

Craps example

If the game being played is craps, then this principle can greatly simplify the computation of the probability of winning in a certain scenario. Specifically, if the first roll is a 4, 5, 6, 8, 9, or 10, then the dice are repeatedly re-rolled until one of two events occurs:

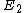Since and are mutually exclusive, the craps principle applies. For example, if the original roll was a 4, then the probability of winning is

This avoids having to sum the infinite series corresponding to all the possible outcomes:

Mathematically, we can express the probability of rolling 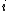ties followed by rolling the point:

The summation becomes an infinite geometric series:

which agrees with the earlier result.

References

1. ^{{Cite web| title = The Craps principle 10/16| author = Susan Holmes| work = statweb.stanford.edu| date = 1998-12-07| accessdate = 2016-03-17| url = http://statweb.stanford.edu/~susan/courses/s116/node63.html}}
2. ^{{cite book|author=Jennifer Ouellette|title=The Calculus Diaries: How Math Can Help You Lose Weight, Win in Vegas, and Survive a Zombie Apocalypse|url=https://books.google.com/books?id=fQzJoqBwtT4C&pg=PT50|date=31 August 2010|publisher=Penguin Publishing Group|isbn=978-1-101-45903-4|pages=50–}}

Notes

{{cite book |author=Pitman, Jim |title=Probability |publisher=Springer-Verlag |location=Berlin |year=1993 |pages= |isbn=0-387-97974-3 |oclc= |doi=}}

3 : Statistical theorems|Probability theorems|Statistical principles

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。