“Cremona group”的意思、由来-开放百科全书

词条

Cremona group

释义

The Cremona group in 2 dimensions
The Cremona group in higher dimensions
De Jonquières groups
References

In algebraic geometry, the Cremona group, introduced by {{harvs|txt|authorlink=Luigi Cremona|last=Cremona|year1=1863|year2=1865}}, is the group of birational automorphisms of the -dimensional projective space over a field . It is denoted by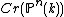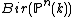

or or .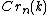

The Cremona group is naturally identified with the automorphism group 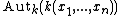of the field of the rational functions in indeterminates over , or in other words a pure transcendental extension of , with transcendence degree .

The projective general linear group of order , of projective transformations, is contained in the Cremona group of order . The two are equal only when or , in which case both the numerator and the denominator of a transformation must be linear.

The Cremona group in 2 dimensions

In two dimensions, Max Noether and Castelnuovo showed that the complex Cremona group is generated by the standard quadratic transformation, along with 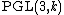, though there was some controversy about whether their proofs were correct, and {{harvtxt|Gizatullin|1983}} gave a complete set of relations for these generators. The structure of this group is still not well understood, though there has been a lot of work on finding elements or subgroups of it.

{{harvtxt|Cantat|Lamy|2010}} showed that the Cremona group is not simple as an abstract group;
Blanc showed that it has no nontrivial normal subgroups that are also closed in a natural topology.
For the finite subgroups of the Cremona group see {{harvtxt|Dolgachev|Iskovskikh|2009}}.

The Cremona group in higher dimensions

There is little known about the structure of the Cremona group in three dimensions and higher though many elements of it have been described. {{harvtxt|Blanc|2010}} showed that it is (linearly) connected, answering a question of {{harvtxt|Serre|2010}}. There is no easy analogue of the Noether–Castelnouvo theorem as {{harvtxt|Hudson|1927}} showed that the Cremona group in dimension at least 3 is not generated by its elements of degree bounded by any fixed integer.

De Jonquières groups

A De Jonquières group is a subgroup of a Cremona group of the following form {{Citation needed|date=August 2018}}. Pick a transcendence basis

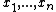for a field extension of . Then a De Jonquières group is the subgroup of automorphisms of mapping the subfield 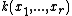into itself for some 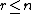. It has a normal subgroup given by the Cremona group of automorphisms of 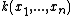over the field 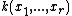, and the quotient group is the Cremona group of 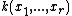over the field . It can also be regarded as the group of birational automorphisms of the fiber bundle .

When and 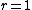the De Jonquières group is the group of Cremona transformations fixing a pencil of lines through a given point, and is the semidirect product of

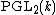and .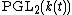

References

{{Citation | last1=Alberich-Carramiñana | first1=Maria | title=Geometry of the plane Cremona maps | publisher=Springer-Verlag | location=Berlin, New York | series=Lecture Notes in Mathematics | isbn=978-3-540-42816-9 | doi=10.1007/b82933 | mr=1874328 | year=2002 | volume=1769}}
{{Citation | last1=Blanc | first1=Jérémy | title=Groupes de Cremona, connexité et simplicité | mr=2662668 | year=2010 | journal=Annales Scientifiques de l'École Normale Supérieure |series=Série 4 | issn=0012-9593 | volume=43 | issue=2 | pages=357–364}}
{{Cite journal| last2=Lamy | first2=Stéphane | last1=Cantat | first1=Serge | title=Normal subgroups in the Cremona group | journal=Acta Mathematica | volume=210 | issue=2013 | pages=31–94 | arxiv=1007.0895 | year=2010| bibcode=2010arXiv1007.0895C }}
{{Citation | last1=Coolidge | first1=Julian Lowell | author1-link=Julian Coolidge | title=A treatise on algebraic plane curves | url=https://books.google.com/books?id=Y7WEf6V0XwgC | publisher=Oxford University Press | isbn=978-0-486-49576-7 | mr=0120551 | year=1931}}
{{Citation | last1=Cremona | first1=L. | title=Sulla trasformazioni geometiche delle figure piane | url=http://it.wikisource.org/wiki/Sulle_trasformazioni_geometriche_delle_figure_piane_%28Cremona%29 | year=1863 | journal=Giornale di matematiche di Battaglini | volume=1 | pages=305–311}}
{{Citation | last1=Cremona | first1=L. | title=Sulla trasformazioni geometiche delle figure piane | url=http://it.wikisource.org/wiki/Sulle_trasformazioni_geometriche_delle_figure_piane,_nota_II_%28Cremona%29 | year=1865 | journal=Giornale di matematiche di Battaglini | volume=3 | pages=269–280, 363–376}}
{{Citation | last1=Demazure | first1=Michel | author1-link=Michel Demazure | title=Sous-groupes algébriques de rang maximum du groupe de Cremona | url=http://www.numdam.org/item?id=ASENS_1970_4_3_4_507_0 | mr=0284446 | year=1970 | journal=Annales Scientifiques de l'École Normale Supérieure |series=Série 4 | issn=0012-9593 | volume=3 | pages=507–588}}
{{Citation | last1=Dolgachev | first1=Igor V. | title=Classical Algebraic Geometry: a modern view | url=http://www.math.lsa.umich.edu/~idolga/CAG.pdf | publisher=Cambridge University Press | isbn=978-1-107-01765-8 | year=2012}}
{{Citation | last1=Dolgachev | first1=Igor V. | last2=Iskovskikh | first2=Vasily A. | title=Algebra, arithmetic, and geometry: in honor of Yu. I. Manin. Vol. I | publisher=Birkhäuser Boston | location=Boston, MA | series=Progr. Math. | doi=10.1007/978-0-8176-4745-2_11 | mr=2641179 | year=2009 | volume=269 | chapter=Finite subgroups of the plane Cremona group | pages=443–548| isbn=978-0-8176-4744-5 | arxiv=math/0610595 }}
{{Citation | last1=Gizatullin | first1=M. Kh. | title=Defining relations for the Cremona group of the plane | doi=10.1070/IM1983v021n02ABEH001789 | mr=675525 | year=1983 | journal=Mathematics of the USSR-Izvestiya | issn=0373-2436 | volume=21 | issue=2 | pages=211–268| bibcode=1983IzMat..21..211G}}
{{Citation | last1=Godeaux | first1=Lucien | title=Les transformations birationelles du plan | publisher=Gauthier-Villars et Cie | series=Mémorial des sciences mathématiques | jfm=53.0595.02 | year=1927 | volume=22}}
{{eom|id=Cremona_group}}
{{eom|id=Cremona_transformation}}
{{Citation | last1=Hudson | first1=Hilda Phoebe | title=Cremona transformations in plane and space | author1-link=Hilda Phoebe Hudson | url=http://www.agnesscott.edu/lriddle/women/abstracts/hudson_cremona.htm | publisher=Cambridge University Press | isbn=978-0-521-35882-8 | id=Reprinted 2012 | year=1927}}
{{Citation | last1=Semple | first1=J. G. | last2=Roth | first2=L. | title=Introduction to algebraic geometry | publisher=The Clarendon Press Oxford University Press | series=Oxford Science Publications | isbn=978-0-19-853363-4 | mr=814690 | year=1985}}
{{Citation | last1=Serre | first1=Jean-Pierre | author1-link=Jean-Pierre Serre | title=A Minkowski-style bound for the orders of the finite subgroups of the Cremona group of rank 2 over an arbitrary field | mr=2567402 | year=2009 | journal=Moscow Mathematical Journal | issn=1609-3321 | volume=9 | issue=1 | pages=193–208}}
{{Citation | last1=Serre | first1=Jean-Pierre | author1-link=Jean-Pierre Serre | title=Le groupe de Cremona et ses sous-groupes finis | url=http://www.bourbaki.ens.fr/TEXTES/1000.pdf | series=Seminaire Bourbaki 1000 | isbn=978-2-85629-291-4 | mr=2648675 | year=2010 | journal=Astérisque | issn=0303-1179 | issue=332 | pages=75–100}}

2 : Birational geometry|Group theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。