平面图形的面积pingmian tuxing de mianji

❶在直角坐标系中计算曲线所围成的平面图形的面积.
若函数f(x),g(x)都是连续的，则曲线y=f (x),y=g (x)与直线x=a,x=b所围成的图形 (见图1)的面积

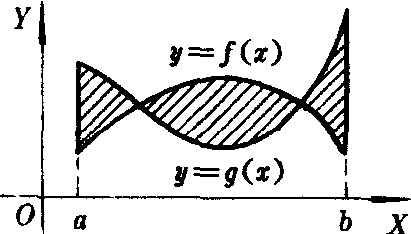
图1

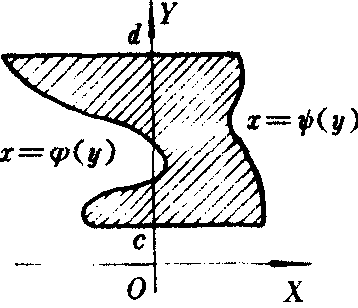
图2

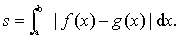
若函数ψ (y) ,ψ (y)都是连续的，则曲线x=ψ(y),x=ψ(y)与直线y=c,y=d的围成的图形(见图2) 的面积

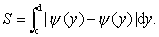
例 求椭圆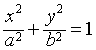的面积.
解 由对称性，只需计算椭圆在第一象限这部分的面积S/4，再四倍即可.

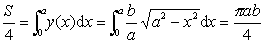
所以X =πab.

❷在极坐标下计算曲线围成的平面图形的面积.
若函数f (θ)在区间 [α,β]上连续，则由极坐标方程r=f (θ),α≤θ≤β表示的曲线与射线θ=α,θ=β (α<β)所围成的平面图形 (见图3) 的面积S=

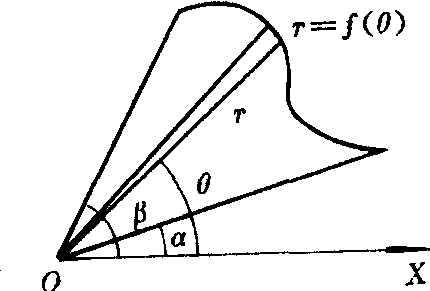
图3

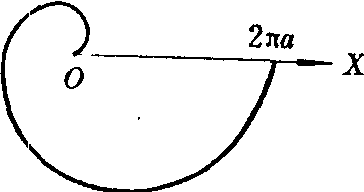
图4

例 求阿基米德螺线r=αθ (0≤θ≤2π)和极轴所围图形的面积，如图4.
解 所求面积