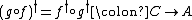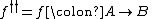“Dagger category”的意思、由来-开放百科全书

词条

Dagger category

释义

Formal definition
Examples
Remarkable morphisms
See also
References

In mathematics, a dagger category (also called involutive category or category with involution ^[1]^[2]) is a category equipped with a certain structure called dagger or involution. The name dagger category was coined by Selinger.^[3]

Formal definition

A dagger category is a category equipped with an involutive functor that is the identity on objects, where is the opposite category.

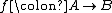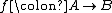In detail, this means that it associates to every morphism in its adjoint such that for all and ,

Note that in the previous definition, the term "adjoint" is used in a way analogous to (and inspired by) the linear-algebraic sense, not in the category-theoretic sense.

Some sources ^[4] define a category with involution to be a dagger category with the additional property that its set of morphisms is partially ordered and that the order of morphisms is compatible with the composition of morphisms, that is 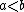implies for morphisms , , whenever their sources and targets are compatible.

Examples

The category Rel of sets and relations possesses a dagger structure i.e. for a given relation in Rel, the relation is the relational converse of . In this example, a self-adjoint morphism is a symmetric relation.
The category Cob of cobordisms is a dagger compact category, in particular it possesses a dagger structure.
The category Hilb of Hilbert spaces also possesses a dagger structure: Given a bounded linear map , the map is just its adjoint in the usual sense.
Any monoid with involution is a dagger category with only one object. In fact, every endomorphism hom-set in a dagger category is not simply a monoid, but a monoid with involution, because of the dagger.
A discrete category is trivially a dagger category.
A groupoid (and as trivial corollary a group) also has a dagger structure with the adjoint of a morphism being its inverse. In this case, all morphisms are unitary.

Remarkable morphisms

In a dagger category , a morphism is called

unitary if ;
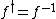self-adjoint if

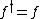
The latter is only possible for an endomorphism .

The terms unitary and self-adjoint in the previous definition are taken from the category of Hilbert spaces where the morphisms satisfying those properties are then unitary and self-adjoint in the usual sense.

References

^[1]^[2]^[3]^[4]

{{nlab|id=dagger-category|title=Dagger category}}

1 : Dagger categories

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Formal definition

Examples

Remarkable morphisms

See also

References