库拉托夫斯基定理kulatuofusiji dingli
图G是平面图的充分必要条件的判定定理.此定理由库拉托夫斯基在1930年给出:图G是平面图当且仅当G不含与K5或K33在2度结点内同构的子图.有两种操作不影响图G的可平面性. 如图中的左图,在给定图G的边上插入(添加)度数为2的点,即将原来的一条边变为两条边;右图则是将关联于度数为2的点的两条边缩成一条边,即删去2度点.如此,可使下图中左图变为右图.
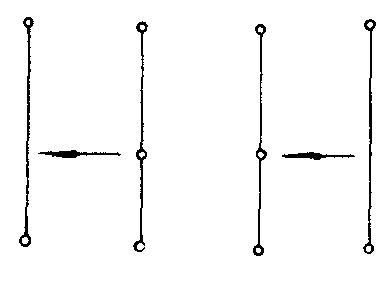
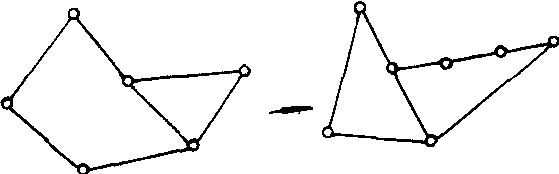
总之,若图G1,G2是同构的,或通过反复插入或删去度数为2的点后得到的图G′1,G2′是同构的.则称G1,G2在2度结点内同构(或同胚).例如,n≥3,C3与任何Cn是2度结点内同构的图.
由库拉托夫斯基定理可和,n≥6,Kn是非平面图.因为,K6删去一点和其关联边后得到的子图是K5,K5非平面图,因之,K6是非平面图,于是,Kn,n≥6都是非平面图.