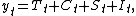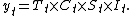- Decomposition based on rates of change
- Decomposition based on predictability
- Examples
- Software
- See also
- References
- Further reading
The decomposition of time series is a statistical task that deconstructs a time series into several components, each representing one of the underlying categories of patterns.[1] There are two principal types of decomposition, which are outlined below.
Decomposition based on rates of change
This is an important technique for all types of time series analysis, especially for seasonal adjustment.[2] It seeks to construct, from an observed time series, a number of component series (that could be used to reconstruct the original by additions or multiplications) where each of these has a certain characteristic or type of behaviour. For example, time series are usually decomposed into:
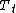, the trend component at time t, which reflects the long-term progression of the series (secular variation). A trend exists when there is a persistent increasing or decreasing direction in the data. The trend component does not have to be linear.[1]
, the cyclical component at time t, which reflects repeated but non-periodic fluctuations. The duration of these fluctuations is usually of at least two years.
, the seasonal component at time t, reflecting seasonality (seasonal variation). A seasonal pattern exists when a time series is influenced by seasonal factors. Seasonality occurs over a fixed and known period (e.g., the quarter of the year, the month, or day of the week).[1]
, the irregular component (or "noise") at time t, which describes random, irregular influences. It represents the residuals or remainder of the time series after the other components have been removed.
Hence a time series using an additive model can be thought of as
whereas a multiplicative model would be
An additive model would be used when the variations around the trend does not vary with the level of the time series whereas a multiplicative model would be appropriate if the trend is proportional to the level of the time series.[3]
Sometimes the trend and cyclical components are grouped into one, called the trend-cycle component. The trend-cycle component can just be referred to as the "trend" component, even though it may contain cyclical behaviour.[3] For example, a seasonal decomposition of time series by Loess (STL)[4] plot decomposes a time series into seasonal, trend and irregular components using loess and plots the components separately, whereby the cyclical component (if present in the data) is included in the "trend" component plot.
Decomposition based on predictability
The theory of time series analysis makes use of the idea of decomposing a times series into deterministic and non-deterministic components (or predictable and unpredictable components).[2] See Wold's theorem and Wold decomposition.
Examples
Kendall shows an example of a decomposition into smooth, seasonal and irregular factors for a set of data containing values of the monthly aircraft miles flown by UK airlines.[5]
In policy analysis, forecasting future production of biofuels is key data for making better decisions, and statistical time series models have recently been developed to forecast renewable energy sources, and a multiplicative decomposition method was designed to forecast future production of biohydrogen. The optimum length of the moving average (seasonal length) and start point, where the averages are placed, were indicated based on the best coincidence between the present forecast and actual values.[6]
Software
An example of statistical software for this type of decomposition is the program BV4.1 that is based on the Berlin procedure.
See also
- Hilbert–Huang transform
- Stochastic drift
References
2. ^1 {{cite book |last=Dodge |first=Y. |year=2003 |title=The Oxford Dictionary of Statistical Terms |location=New York |publisher=Oxford University Press |isbn=0-19-920613-9 }}
3. ^1 {{Cite web|url=https://www.otexts.org/fpp/6/1|title=6.1 Time series components {{!}} OTexts|website=www.otexts.org|access-date=2016-05-18}}
4. ^{{Cite web|url=https://www.otexts.org/fpp/6/5|title=6.5 STL decomposition {{!}} OTexts|website=www.otexts.org|access-date=2016-05-18}}
5. ^{{cite book |last=Kendall |first=M. G. |year=1976 |title=Time-Series |edition=Second |publisher=Charles Griffin |isbn=0-85264-241-5 |at=(Fig. 5.1) }}
6. ^1 {{cite journal |last1=Asadi |first1=Nooshin |last2=Karimi Alavijeh |first2=Masih |last3=Zilouei |first3=Hamid |title=Development of a mathematical methodology to investigate biohydrogen production from regional and national agricultural crop residues: A case study of Iran |journal=International Journal of Hydrogen Energy |date=2016 |doi=10.1016/j.ijhydene.2016.10.021 |url=https://www.researchgate.net/publication/309382052}}
Further reading
- {{cite book |last=Enders |first=Walter |chapter=Models with Trend |title=Applied Econometric Time Series |location=New York |publisher=Wiley |edition=Second |year=2004 |isbn=0-471-23065-0 |pages=156–238 }}
- 1978 World Series of Poker
- 1978 World Snooker Championship
- 1978 World Sportscar Championship
- 1978 World Women's Handball Championship
- 1978 WSOP
- 1978 Wycombe by-election
- 1978–1990 (Go-Betweens album)
- 1978–79 2. Bundesliga
- 1978–79 AHL season
- 1978–79 Alpha Ethniki
- 1978–79 Boston Bruins season
- 1978–79 Boston College basketball point shaving scandal
- 1978–79 British Home Championship
- 1978–79 Cuban National Series
- 1978–79 Divizia A
- 1978–79 European Cup
- 1978–79 European Cup Winners' Cup
- 1978–79 FIS Alpine Ski World Cup
- 1978–79 French Division 1
- 1978–79 Honduran Liga Nacional
- 1978–79 in English football
- 1978–79 in Scottish football
- 1978–79 La Liga
- 1978–79 Montreal Canadiens season
- 1978–79 NBA season