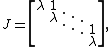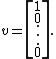“Defective matrix”的意思、由来-开放百科全书

词条

Defective matrix

释义

Jordan block
Example
See also
Notes
References

In linear algebra, a defective matrix is a square matrix that does not have a complete basis of eigenvectors, and is therefore not diagonalizable. In particular, an n × n matrix is defective if and only if it does not have n linearly independent eigenvectors.^[1] A complete basis is formed by augmenting the eigenvectors with generalized eigenvectors, which are necessary for solving defective systems of ordinary differential equations and other problems.

A defective matrix always has fewer than n distinct eigenvalues, since distinct eigenvalues always have linearly independent eigenvectors. In particular, a defective matrix has one or more eigenvalues λ with algebraic multiplicity m > 1 (that is, they are multiple roots of the characteristic polynomial), but fewer than m linearly independent eigenvectors associated with λ. If the algebraic multiplicity of λ exceeds its geometric multiplicity (that is, the number of linearly independent eigenvectors associated with λ), then λ is said to be a defective eigenvalue.^[1] However, every eigenvalue with algebraic multiplicity m always has m linearly independent generalized eigenvectors.

A Hermitian matrix (or the special case of a real symmetric matrix) or a unitary matrix is never defective; more generally, a normal matrix (which includes Hermitian and unitary as special cases) is never defective.

Jordan block

Any nontrivial Jordan block of size 2×2 or larger (that is, not completely diagonal) is defective. (A diagonal matrix is a special case of the Jordan normal form and is not defective.) For example, the n × n Jordan block,

has an eigenvalue, λ, with algebraic multiplicity n, but only one distinct eigenvector,

In fact, any defective matrix has a nontrivial Jordan normal form, which is as close as one can come to diagonalization of such a matrix.

Example

A simple example of a defective matrix is:

which has a double eigenvalue of 3 but only one distinct eigenvector

(and constant multiples thereof).

Notes

1. ^¹{{harvtxt|Golub|Van Loan|1996|p=316}}

References

{{ citation | first1 = Gene H. | last1 = Golub | first2 = Charles F. | last2 = Van Loan | year = 1996 | isbn = 978-0-8018-5414-9 | title = Matrix Computations | edition = 3rd | publisher = Johns Hopkins University Press | location = Baltimore }}
{{cite book|first=Gilbert|last= Strang|title=Linear Algebra and Its Applications|edition=3rd |publisher=Harcourt|location= San Diego|year= 1988|isbn=978-970-686-609-7}}

1 : Linear algebra

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Jordan block

Example

See also

Notes

References