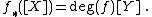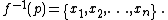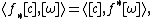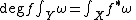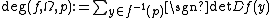“Degree of a continuous mapping”的意思、由来-开放百科全书

词条

Degree of a continuous mapping

释义

Definitions of the degree
From Sⁿ to Sⁿ Between manifolds Algebraic topology Differential topology Maps from closed region
Properties
See also
Notes
References
External links

{{About|the term "degree" as used in algebraic topology||Degree (disambiguation)}}

In topology, the degree of a continuous mapping between two compact oriented manifolds of the same dimension is a number that represents the number of times that the domain manifold wraps around the range manifold under the mapping. The degree is always an integer, but may be positive or negative depending on the orientations.

The degree of a map was first defined by Brouwer,^[1] who showed that the degree is homotopy invariant (invariant among homotopies), and used it to prove the Brouwer fixed point theorem. In modern mathematics, the degree of a map plays an important role in topology and geometry. In physics, the degree of a continuous map (for instance a map from space to some order parameter set) is one example of a topological quantum number.

Definitions of the degree

From Sⁿ to Sⁿ

The simplest and most important case is the degree of a continuous map from the -sphere to itself (in the case , this is called the winding number):

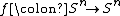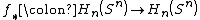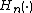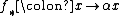Let be a continuous map. Then induces a homomorphism , where is the th homology group. Considering the fact that , we see that must be of the form for some fixed .

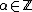This is then called the degree of .

Between manifolds

Algebraic topology

Let X and Y be closed connected oriented m-dimensional manifolds. Orientability of a manifold implies that its top homology group is isomorphic to Z. Choosing an orientation means choosing a generator of the top homology group.

A continuous map f : X→Y induces a homomorphism f_* from H_m(X) to H_m(Y). Let [X], resp. [Y] be the chosen generator of H_m(X), resp. H_m(Y) (or the fundamental class of X, Y). Then the degree of f is defined to be f_*([X]). In other words,

If y in Y and f ⁻¹(y) is a finite set, the degree of f can be computed by considering the m-th local homology groups of X at each point in f ⁻¹(y).

Differential topology

In the language of differential topology, the degree of a smooth map can be defined as follows: If f is a smooth map whose domain is a compact manifold and p is a regular value of f, consider the finite set

By p being a regular value, in a neighborhood of each x_i the map f is a local diffeomorphism (it is a covering map). Diffeomorphisms can be either orientation preserving or orientation reversing. Let r be the number of points x_i at which f is orientation preserving and s be the number at which f is orientation reversing. When the domain of f is connected, the number r − s is independent of the choice of p (though n is not!) and one defines the degree of f to be r − s. This definition coincides with the algebraic topological definition above.

The same definition works for compact manifolds with boundary but then f should send the boundary of X to the boundary of Y.

One can also define degree modulo 2 (deg₂(f)) the same way as before but taking the fundamental class in Z₂ homology. In this case deg₂(f) is an element of Z₂ (the field with two elements), the manifolds need not be orientable and if n is the number of preimages of p as before then deg₂(f) is n modulo 2.

Integration of differential forms gives a pairing between (C^∞-)singular homology and de Rham cohomology: 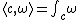, where is a homology class represented by a cycle and 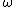a closed form representing a de Rham cohomology class. For a smooth map f : X→Y between orientable m-manifolds, one has

where f_* and f* are induced maps on chains and forms respectively. Since f_*[X] = deg f · [Y], we have

for any m-form ω on Y.

Maps from closed region

If 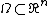is a bounded region, 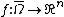smooth, a regular value of and

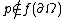, then the degree 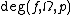is defined

by the formula

where is the Jacobi matrix of in .

This definition of the degree may be naturally extended for non-regular values such that 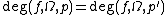where is a point close to .

The degree satisfies the following properties:^[2]

If 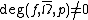, then there exists 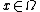such that .
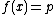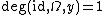for all .
Decomposition property:

, if are disjoint parts of and .

Homotopy invariance: If and are homotopy equivalent via a homotopy such that and , then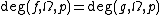
The function 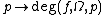is locally constant on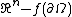

These properties characterise the degree uniquely and the degree may be defined by them in an axiomatic way.

In a similar way, we could define the degree of a map between compact oriented manifolds with boundary.

Properties

The degree of a map is a homotopy invariant; moreover for continuous maps from the sphere to itself it is a complete homotopy invariant, i.e. two maps 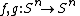are homotopic if and only if .

In other words, degree is an isomorphism between 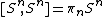and .

Moreover, the Hopf theorem states that for any -dimensional closed oriented manifold M, two maps are homotopic if and only if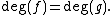

A self-map 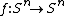of the n-sphere is extendable to a map 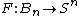from the n-ball to the n-sphere if and only if . (Here the function F extends f in the sense that f is the restriction of F to .)

Notes

1. ^{{cite journal | last = Brouwer | first = L. E. J. | authorlink = Luitzen Egbertus Jan Brouwer | title = Über Abbildung von Mannigfaltigkeiten | journal = Mathematische Annalen | volume = 71 | issue = 1 | pages = 97–115 | year = 1911 | url = http://www.springerlink.com/content/h15uqp1w28862q47 | doi=10.1007/bf01456931}}
2. ^{{cite book|last=Dancer|first=E. N.|title=Calculus of Variations and Partial Differential Equations|year=2000|publisher=Springer-Verlag|isbn=3-540-64803-8|pages=185–225}}

References

{{cite book|author=Flanders, H.|title=Differential forms with applications to the physical sciences|publisher=Dover|year=1989}}
{{cite book|author=Hirsch, M.|title=Differential topology|publisher=Springer-Verlag|year=1976|isbn=0-387-90148-5}}
{{cite book|author=Milnor, J.W.|title=Topology from the Differentiable Viewpoint|publisher=Princeton University Press|year=1997|isbn=978-0-691-04833-8}}
{{cite book|author1=Outerelo, E. |author2=Ruiz, J.M. |title=Mapping Degree Theory|publisher=American Mathematical Society|year=2009|isbn=978-0-8218-4915-6}}

External links

{{springer|title=Brouwer degree|id=p/b130260}}
TopDeg: Software tool for computing the topological degree of a continuous function (LGPL-3)

3 : Algebraic topology|Differential topology|Continuous mappings

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。