1. Example

2. See also

3. References

In mathematics, a nonempty collection of sets is called a δ-ring (pronounced delta-ring) if it is closed under union, relative complementation, and countable intersection:

1. if
2. if
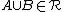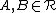
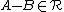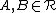
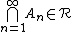3. if 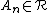for all

If only the first two properties are satisfied, then is a ring but not a δ-ring. Every σ-ring is a δ-ring, but not every δ-ring is a σ-ring.

δ-rings can be used instead of σ-fields in the development of measure theory if one does not wish to allow sets of infinite measure.

Example

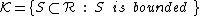is a δ-ring.

It is not a σ-ring since

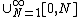is not bounded.

See also

• Ring of sets
• Sigma field
• Sigma ring

References

• Cortzen, Allan. "Delta-Ring." From MathWorld—A Wolfram Web Resource, created by Eric W. Weisstein. http://mathworld.wolfram.com/Delta-Ring.html

• Community rail
• Community railway
• Community Recognition
• Community recognition
• Community Reference Laboratory for Avian Influenza
• Community reinvestment
• Community Research & Development Information Service
• Community Research & Development Information Service (CORDIS)
• Community Resources against Street Hoodlums
• Community Rowing, Inc.
• Community Rule
• Community sale
• Community School Disctrict 99
• Community School District 18
• Community School of Auchterarder
• Community School of Music and Arts
• Community School of Music and Arts at Finn Center
• Community School (Sun Valley, Idaho)
• Community School (Teaneck, New Jersey)
• Community School, Teaneck, New Jersey
• Community School, Tehran
• Community Security Trust
• Community sentence
• Community sentences
• Community Service Foundation