异面直线yimian zhixian

不在同一平面内的两条直线.
画异面直线时，要用辅助平面作衬托，以显示它们不共面的特点(图1).

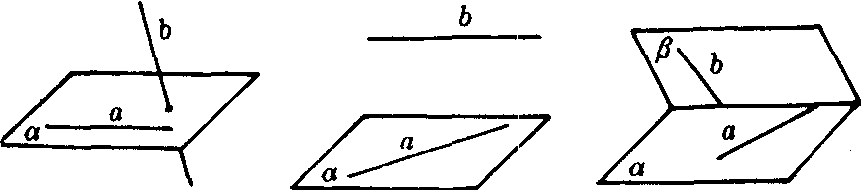
图1

证明两条直线是异面直线通常采用反证法.有时也可使用判定定理“平面内一点与平面外一点的连线，与平面内不经过该点的直线是异面直线”.
例 已知两平面a,β相交于直线a，直线b在a内与a交于A点，直线c在β内与a平行(如图2).求证直线b和c是异面直线.

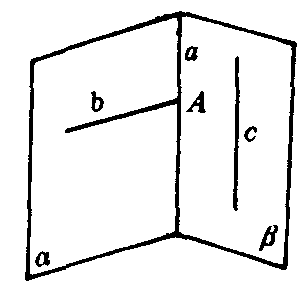
图2

证法1 证明直线b与c既不平行也不相交.
假设b∥c.因为a∥c，所以b∥a.与已知条件b和a相交矛盾，所以b与c不平行.
假设b∩c=B.因为a∥c，所以点B与点A不重合.又因为b∩a=A，所以直线b上有两个点在β内，因此b⊂β.由已知b⊂a，所以b是a和β的交线.于是b与a重合.与已知条件b与a相交矛盾.所以b与c不相交.
因为直线b与c既不平行也不相交，所以b与c是异面直线.
证法2 证明b与c不共面.
假设b与c在同一平面γ内.则平面γ过直线c和点A，但已知β过c和A.由推论1可知γ和β重合.于是b⊂β.因为a和β都经过两条相交直线a和b.由推论2可知a和β重合.与已知条件a,β相交矛盾.所以b与c不能共面，即b与c是异面直线.
证法3 在直线b上除A点外任取一点B.因为A∈β，所以Bβ(若B∈β，则b⊂β，于是b与a重合，与b与a相交矛盾).因此b是平面β内一点A与平面外一点B的连线.因为a∥c,A∈a，所以Ac.又c⊂β，即c是平面β内不过A点的直线.所以b和c是异面直线.