“Direct image functor”的意思、由来-开放百科全书

词条

Direct image functor

释义

Definition
Example Variants
Higher direct images
Properties
See also
References

In mathematics, in the field of sheaf theory and especially in algebraic geometry, the direct image functor generalizes the notion of a section of a sheaf to the relative case.

Definition

Let f: X → Y be a continuous mapping of topological spaces, and Sh(–) the category of sheaves of abelian groups on a topological space. The direct image functor

sends a sheaf F on X to its direct image presheaf

which turns out to be a sheaf on Y.

This assignment is functorial, i.e. a morphism of sheaves φ: F → G on X gives rise to a morphism of sheaves f_∗(φ): f_∗(F) → f_∗(G) on Y.

Example

If Y is a point, then the direct image equals the global sections functor.

Let f: X → Y be a continuous map of topological spaces or a morphism of schemes. Then the exceptional inverse image is a functor

f^!: D(Y) → D(X).

Variants

A similar definition applies to sheaves on topoi, such as etale sheaves. Instead of the above preimage f⁻¹(U) the fiber product of U and X over Y is used.

Higher direct images

The direct image functor is left exact, but usually not right exact. Hence one can consider the right derived functors of the direct image. They are called higher direct images and denoted R^q f_∗.

One can show that there is a similar expression as above for higher direct images: for a sheaf F on X, R^q f_∗(F) is the sheaf associated to the presheaf

Properties

The direct image functor is right adjoint to the inverse image functor, which means that for any continuous and sheaves respectively on X, Y, there is a natural isomorphism:

.

If f is the inclusion of a closed subspace X ⊂ Y then f_∗ is exact. Actually, in this case f_∗ is an equivalence between sheaves on X and sheaves on Y supported on X. It follows from the fact that the stalk of is if 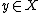and zero otherwise (here the closedness of X in Y is used).

References

{{Citation | last1=Iversen | first1=Birger | title=Cohomology of sheaves | publisher=Springer-Verlag | location=Berlin, New York | series=Universitext | isbn=978-3-540-16389-3 | mr=842190 | year=1986}}, esp. section II.4

2 : Sheaf theory|Continuous mappings

随便看